题目内容
【题目】如图，已知AB是⊙O的弦，AC是⊙O的直径,D为⊙O上一点，过D作⊙O的切线交BA的延长线于P,且DP⊥BP于P.若PD+PA=6，AB=6，则⊙O的直径AC的长为（ ）
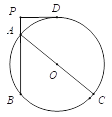
A. 5 B. 8 C. 10 D. 12
【答案】C
【解析】分析：通过切线的性质表示出EC的长度，用相似三角形的性质表示出OE的长度，由已知条件表示出OC的长度即可通过勾股定理求出结果.
详解：如图：连接BC，并连接OD交BC于点E：
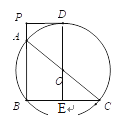
∵DP⊥BP，AC为直径；
∴∠DPB=∠PBC=90°.
∴PD∥BC,且PD为⊙O的切线.
∴∠PDE=90°=∠DEB,
∴四边形PDEB为矩形，
∴AB∥OE，且O为AC中点，AB=6.
∴PD=BE=EC.
∴OE=
AB=3.
设PA=x，则OD=DE-OE=6+x-3=3+x=OC，EC=PD=6-x.
.在Rt△OEC中:
,
即：
，解得x=2.
所以AC=2OC=2×（3+x）=10.
练习册系列答案
字词句段篇系列答案
相关题目
