题目内容
【题目】如图,直线PC交⊙O于A,C两点,AB是⊙O的直径,AD平分∠PAB交⊙O于点D,过D作DE垂直PA,垂足为E.
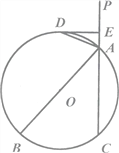
(1)求证:DE是⊙O的切线;
(2)若AE=1,AC=4,求直径AB的长.
【答案】(1)见解析;(2)6.
【解析】分析:
(1)如下图,连接OD,由已知条件易得∠DAE=∠DAO,∠DAO=∠ADO,∠DAE+∠ADE=90°,由此可得∠ADO+∠ADE=90°=∠ODE,从而可得DE是⊙O的切线;
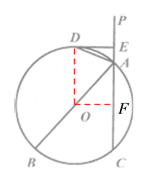
(2)如下图,过点O作OF⊥AC于点F,则易得AF=![]() AC=2,四边形OFED是矩形,从而可得OD=EF=AE+AF=1+2=3,由此可得AB=2OD=6.
AC=2,四边形OFED是矩形,从而可得OD=EF=AE+AF=1+2=3,由此可得AB=2OD=6.
详解:
(1)如下图,连接OD,
∵AD平分∠PAB,
∴∠PAD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠PAD=∠ODA,
∵DE⊥PA,
∴∠DEA=∠EAD+∠EDA=90°,
∴∠ODA+∠EDA=90°,
∴DE是⊙O的切线
(2)作OF⊥AC,
∴AF=CF=2,∠OFE=90°,
又∵∠DEA=∠ODE=90°,
∴四边形OFED为矩形,
∴OD=EF=AE+AF=3,
∴AB=2OD=6.

 口算小状元口算速算天天练系列答案
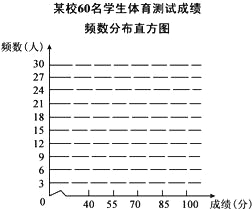
口算小状元口算速算天天练系列答案【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级的各班分别随机抽取了5名男生和5名女生,组成了一个容量为60的样本,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
成绩 | 划记 | 频数 | 百分比 |
优秀 | 正正正 | a | 30% |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 15% |
不合格 |
| 3 | 5% |
合计 | 60 | 60 | 100% |
(说明:40﹣﹣﹣55分为不合格,55﹣﹣﹣70分为合格,70﹣﹣﹣85分为良好,85﹣﹣﹣100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=_____,b=_____;
(2)请根据频数分布表,画出相应的频数分布直方图;
(3)如果该校八年级共有150名学生,根据以上数据,估计该校八年级学生身体素质良好及以上的人数为_____.