ÌâÄżÄÚÈĘ
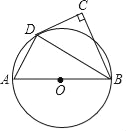
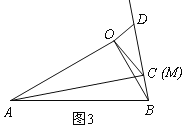
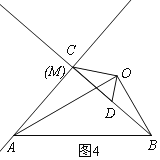
ĄŸÌâÄżĄżÈçÍŒŁŹÒŃÖȘABÊÇĄŃO”ÄÖ±Ÿ¶ŁŹBCÓëĄŃOÏàÇĐÓÚ”ăBŁŹCDÓëĄŃOÏàÇĐÓÚ”ăDŁŹÁŹœáADŁź
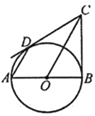
(1)ÇóÖ€ŁșADĄÎOCŁź
(2)ĐĄŽÏÓëĐĄĂśÔÚŚöŐâžöÌâÄż”ÄʱșòŁŹ¶ÔĄÏCDAÓëĄÏAOCÖźŒä”ÄčŰÏ”œűĐĐÁËÌœŸżŁș
ĐĄŽÏË”ŁŹĄÏCDA+ĄÏAOC”ÄÖ”ÊÇÒ»žöč̶š”ÄÖ”Ł»
ХÜ˔ŁŹĄÏCDA+ĄÏAOC”ÄÖ”ËæĄÏA¶ÈÊę”ı仯¶ű±ä»Ż.
ÈôĄÏCDA+ĄÏAOC”ÄÖ”ÎȘyŁŹĄÏA¶ÈÊęÎȘxŁźÄăÈÏÎȘËûĂÇÖźÖĐËË””ÄÊÇŐęÈ·”Ä?ÈôÄăÈÏÎȘĐĄŽÏË””ÄŐęÈ·ŁŹÇëÄăÇółöŐâžöč̶šÖ”ŁșÈôÄăÈÏÎȘХÜ˔”ÄŐęÈ·ŁŹÇëÄăÇółöyÓëxÖźŒä”ÄčŰÏ”Łź
ĄŸŽđ°žĄż(1)րÜŒûœâÎöŁ»(2)ĐĄŽÏË””ĶԣŹĄÏCDA+ĄÏAOC”ÄÖ”ÊÇÒ»žöč̶š”ÄÖ”ŁŹ270Ąă.
ĄŸœâÎöĄż
Łš1Ł©ÁŹœáODŁŹžùŸĘÇĐÏßĐÔÖÊ”ĂĄÏODC=ĄÏOBC=90ĄăŁŹÓÉÈ«”ÈÈęœÇĐÎĆжšHL”ĂRtĄśODCĄŐRtĄśOBCŁŹžùŸĘÈ«”ÈÈęœÇĐÎĐÔÖÊ”ĂĄÏDOC=ĄÏBOCŁŹžùŸĘÈęœÇĐÎÄÚœÇșͶšÀíșÍÆœœÇ”ĂĄÏODA+ĄÏOAD=ĄÏDOC+ĄÏBOCŁŹŽÓ¶űżÉ”ĂĄÏODA=ĄÏDOCŁŹÓÉÆœĐĐÏßĆжšŒŽżÉ”ĂÖ€.
Łš2Ł©ĐĄŽÏË””ĶԣŹĄÏCDA+ĄÏAOC”ÄÖ”ÊÇÒ»žöč̶š”ÄÖ”ŁŹÀíÓÉÈçÏÂŁșžùŸĘÌâÒâżÉ”Ă90Ąă+x+ĄÏAOC=yŁŹŒŽx+ĄÏAOC=y-90ĄăŁŹÓÉÆœĐĐÏßĐÔÖÊ”ĂĄÏOAD+ĄÏAOC=180ĄăŁŹŒŽx+ĄÏAOC=180ĄăŁŹÁœÊœÁȘÁążÉ”Ă90Ąă+180Ąă=y=270Ąă.
œâŁș(1)ÁŹœáODŁŹÈçÍŒŁș
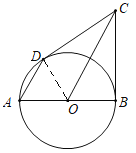 ŁŹ
ŁŹ
Ąß BCÓëĄŃOÏàÇĐÓÚ”ăBŁŹCDÓëĄŃOÏàÇĐÓÚ”ăDŁŹ
ĄàĄÏODC=ĄÏOBC=90ĄăŁŹ
ĄßOD=OBŁŹOC=OCŁŹ
ĄàRtĄśODCĄŐRtĄśOBC(HL)ŁŹ
ĄàĄÏDOC=ĄÏBOCŁŹ
ĄßOA=ODŁŹ
ĄàĄÏODA=ĄÏOADŁŹ
ĄßĄÏAOD+ĄÏODA+ĄÏOAD=180ĄăŁŹĄÏAOD+ĄÏDOC+ĄÏBOC=180ĄăŁŹ
ĄàĄÏODA+ĄÏOAD=ĄÏDOC+ĄÏBOCŁŹ
ĄàĄÏODA=ĄÏDOCŁŹ
ĄàADĄÎCO.
(2)ĐĄŽÏË””ĶԣŹĄÏCDA+ĄÏAOC”ÄÖ”ÊÇÒ»žöč̶š”ÄÖ”ŁŹÀíÓÉÈçÏÂŁș
ĄßĄÏCDA+ĄÏAOC=yŁŹĄÏA=xŁŹ
ĄàĄÏODA=ĄÏOAD=xŁŹĄÏODC+ĄÏODA+ĄÏAOC=yŁŹ
ĄßĄÏODC=90ĄăŁŹ
Ąà90Ąă+x+ĄÏAOC=yŁŹ
ŒŽx+ĄÏAOC=y-90ĄăŁŹ
ĄßADĄÎCOŁŹ
ĄàĄÏOAD+ĄÏAOC=180ĄăŁŹ
ŒŽx+ĄÏAOC=180ĄăŁŹ
Ąà90Ąă+180Ąă=yŁŹ
ŒŽy=270ĄăŁŹ
ĄàĐĄŽÏË””ĶԣŹĄÏCDA+ĄÏAOC”ÄÖ”ÊÇÒ»žöč̶š”ÄÖ”.

ĄŸÌâÄżĄż2019Äê3ÔÂ30ÈŐŁŹËÄŽšÊĄÁčÉœÖĘÄŸÀïÏŰŸłÄÚ·ąÉúÉÁÖ»đÔÖŁŹ30ĂûŚóÓÒ”ÄÆË»đÓąĐÛÎțÉüŁŹÈĂÈ˞ДœÍŽĐÄŁŹÒČÔَΞűÎÒĂǔķÀ»đ°ČÈ«ÒâʶÇĂÏìŸŻÖÓŁźÎȘÁËŒÓǿѧÉú”Ä·À»đ°ČÈ«ÒâʶŁŹÄłĐŁŸÙĐĐÁËÒ»ŽÎĄ°·À»đ°ČÈ«ÖȘʶŸșÈüĄ±ŁšÂú·Ö100·ÖŁ©ŁŹÈüșóŽÓÖĐłéÈĄÁËČż·ÖѧÉú”ÄłÉŒšœűĐĐŐûÀíŁŹČąÖÆŚśÁËÈçÏÂČ»ÍêŐû”ÄÍłŒÆÍŒ±íŁș
Śé±đ | łÉŒšx/·Ö | ŚéÖĐÖ” |
A | 50ĄÜxŁŒ60 | 55 |
B | 60ĄÜxŁŒ70 | 65 |
C | 70ĄÜxŁŒ80 | 75 |
D | 80ĄÜxŁŒ90 | 85 |
E | 90ĄÜxŁŒ100 | 95 |
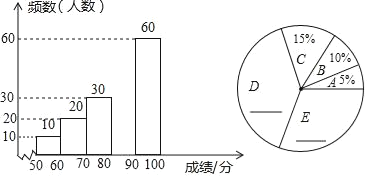
ÇëžùŸĘÍŒ±íÌáč©”ÄĐĆÏąŁŹœâŽđÏÂÁĐžśÌâŁș
Łš1Ł©ČčÈ«Æ”Êę·ÖČŒÖ±·œÍŒșÍÉÈĐÎÍłŒÆÍŒŁ»
Łš2Ł©·ÖÊę¶Î80ĄÜxŁŒ90¶ÔÓŠÉÈĐΔÄÔČĐĜǔĶÈÊęÊÇĄĄ ĄĄĄăŁŹËùłéÈĄ”ÄѧÉúŸșÈüłÉŒš”ÄÖĐλÊęÂäÔÚĄĄ ĄĄÇűŒäÄÚŁ»
Łš3Ł©Èôœ«ĂżŚé”ÄŚéÖĐÖ”ŁšžśŚéÁœžö¶Ë”ă”ÄÊę”ÄÆœŸùÊ꣩Žú±ížśŚéÿλѧÉú”ÄŸșÈüłÉŒšŁŹÇëÄăčÀŒÆžĂĐŁČÎÈüѧÉú”ÄÆœŸùłÉŒšŁź