Question

【题目】为迎接“五一”劳动节，某中学组织了甲、乙两个义务劳动小组，甲组x人，乙组y人，到“中华路”和“青年路”打扫卫生，根据打扫卫生的进度，学校随时调整两组人数，如果从甲组调50人去乙组，则乙组人数为甲组人数的2倍；如果从乙组调m人去甲组，则甲组人数为乙组人数的3倍．

(1)求出x与m之间的函数表达式．

(2)问：当m为何值时，甲组人数最少，最少是多少人？

Answer 1

【答案】（1）x＝m＋90.（2）当m＝5时，甲组人数最少，最少是94人．

【解析】试题分析：（1）等量关系为：（甲组人数-50）×2=乙组人数+50，甲组人数+m=（乙组人数-m）×3．据此列出方程组求出x与m的关系式．

（2）根据（1）中得出的关系式，来判断符合条件的x和m的取值．

试题解析：（1）由题意得方程组：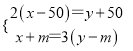

整理得：

①×3-②得：5x=450+4m，

∴x=m+90（得到5x=450+4m或其变形式皆给分）．

（2）由x=m+90知x随m增大而增大，

又因x，m，y均为正整数，

所以当m=5时，x取得最小值．

其最小值为×5+90=94，

此时y=38适合题意．

答：当m=5时，甲组人数最少，最少为94人．