题目内容
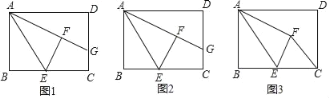
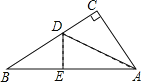
【题目】如图，E、F分别是AD和BC上的两点，EF将四边形ABCD分成两个边长为5cm的正方形，∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm，点P从点H出发，沿HD以lcm/s的速度运动，同时点Q从点A出发，沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.
(1)如图1，点Q在AB上运动，连结QF，当t= 时，QF//EP;
(2)如图2，若QE⊥EP，求出t的值;
(3)试探究:当t为何值时，
的面积等于
面积的
.
【答案】（1）
；（2）
；（3）t=0.5，
，
.
【解析】
(1)假设EP∥FQ，得到∠PEF=∠EFQ，由等角的余角相等，得∠QFB=∠DEP，通过正切关系，得到BQ与PD关系，求出t；
(2)通过△QEF≌△PED，得到FQ与PD间关系，进而求出t的值；
(3)分类讨论：①当点Q在AB上时；②当点Q在BF上时，③当点Q在CF上时，分别求出t．
(1)由题意知：ED=FB=5cm，∠D=∠B=∠DEF=∠EFB=90°，
如图，若EP∥FQ时，∠PEF=∠EFQ，
∴∠DEP=∠DEF-∠PEF=∠EFB-∠EFQ=∠QFB，
∴tan∠QFB=
，
所以BQ=DP，
∵BQ=5-5t，DP=DC-CH-PH=5-1-t=4-t，
∴5-5t=4-t，
∴t=，
故答案为：；
(2)如图所示，若QE⊥EP，则∠QEP+∠FEP=90°，
又∵∠DEP+∠PEF=90°，
∴∠QEF=∠DEP，
在△QEF和△PED中，
，
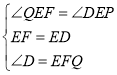∴△QEF≌△PED，
∴QF=DP，
∵FQ=10-5t，DP=4-t，
∴10-5t=4-t，
；
(3)①如图所示，过Q做QM⊥EF，垂足为M，
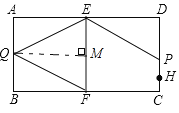
由于四边形ABFE是正方形，所以QM=AE=5cm，
当0＜t≤1时，
，
，
当
，
解得，t=0.5；
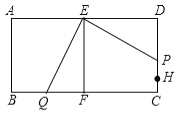
②当1＜t≤2时，
，
，
，
，
解得： ；
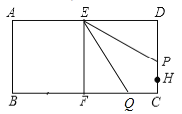
③当2＜t≤3时，
，
，
解得： ，
综合上述：t=0.5，，.
