题目内容
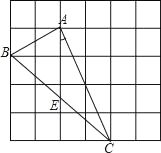
【题目】如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )

A. 12B. 14C. 16D. 18
【答案】D
【解析】
连接AE和CD,要求三角形DEF的面积,可以分成三部分(△FCD+△FCE+△DCE)来分别计算,三角形ABC是一个重要的条件,抓住图形中与它同高的三角形进行分析计算,即可解得△DEF的面积.
解:连接AE和CD,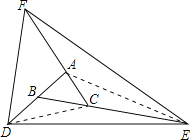
∵BD=AB,
∴S△ABC=S△BCD=1,S△ACD=1+1=2,
∵AF=3AC,
∴FC=4AC,
∴S△FCD=4S△ACD=4×2=8,
同理可以求得:S△ACE=2S△ABC=2,则S△FCE=4S△ACE=4×2=8;
S△DCE=2S△BCD=2×1=2;
∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18.
故选:D.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目