题目内容
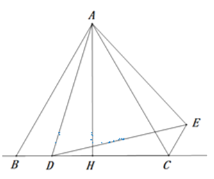
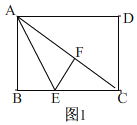
【题目】如图,在矩形ABCD中,E是BC上一动点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,AB=3,AD=4.
(1)如图,当∠DAG=30° 时,求BE的长;
(2)如图,当点E是BC的中点时,求线段GC的长;
(3)如图,点E在运动过程中,当△CFE的周长最小时,直接写出BE的长.
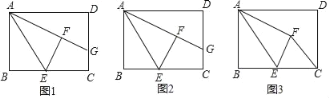
【答案】(1)∵四边形ABCD是矩形,
∴∠BAD=90,
∵∠DAG=30,
∴∠BAG=60
由折叠知,∠BAE=![]() ∠BAG=30,
∠BAG=30,
在Rt△BAE中,∠BAE=30,AB=3,
∴BE=![]()
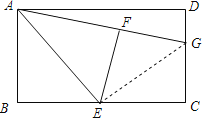
(2)如图,连接GE,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90,
∴∠EFG=90,
∵在Rt△GFE和Rt△GCE中,
EG=EG,
EF=EC,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
设GC=x,则AG=3+x,DG=3x,
在Rt△ADG中,42+(3x)2=(3+x)2,
解得x=![]() .
.
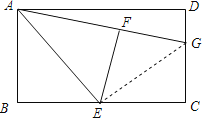
(3)如图1,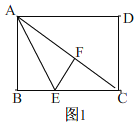
由折叠知,∠AFE=∠B=90,EF=BE,
∴EF+CE=BE+CE=BC=AD=4,
∴当CF最小时,△CEF的周长最小,
∵∠AFE=90,
∴点A,F,C在同一条直线上时,CF最小,
由折叠知,AF=AB=3,
在Rt△ABC中,AB=3,BC=AD=4,
∴AC=5,
∴CF=ACAF=2,
在Rt△CEF中,
.EF2+CF2=CE2,
∴BE2+CF2=(4BE)2,
∴BE2+22=(4BE)2,
∴BE=![]() .
.
【解析】
试题(1)先确定出∠BAE=30°,再利用含30°的直角三角形的性质即可得出结论
(2)连接GE,根据点E是BC的中点以及翻折的性质可以求出BE=EF=EC,然后利用“HL”证明△GFE和△GCE全等,根据全等三角形对应边相等即可得证FG=CG,设GC=x,表示出AG、DG,然后在Rt△ADG中,利用勾股定理列式进行计算即可得解;
(3)先判断出EF⊥AC时,△CEF的周长最小,最后用勾股定理即可得出结论.
试题解析:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠DAG=30°,
∴∠BAG=60°
由折叠知,∠BAE=![]() ∠BAG=30°,
∠BAG=30°,
在Rt△BAE中,∠BAE=30°,AB=3,
∴BE=![]() ;
;
(2)如图,/span>连接GE,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,![]() ,
,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
设GC=x,则AG=3+x,DG=3x,
在Rt△ADG中,42+(3x)2=(3+x)2,
解得x=![]() .
.
(3)如图1,
由折叠知,∠AFE=∠B=90°,EF=BE,
∴EF+CE=BE+CE=BC=AD=4,
∴当CF最小时,△CEF的周长最小,
∵∠AFE=90°,
∴点A,F,C在同一条直线上时,CF最小,
由折叠知,AF=AB=3,
在Rt△ABC中,AB=3,BC=AD=4,
∴AC=5,
∴CF=ACAF=2,
在Rt△CEF中,EF2+CF2=CE2,
∴BE2+CF2=(4BE)2,
∴BE2+22=(4BE)2,
∴BE=![]() .
.

【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?