Question

【题目】如图,已知圆锥的底面半径是2,母线长是6.

（1）求这个圆锥的高和其侧面展开图中∠ABC的度数；

（2）如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.

Answer 1

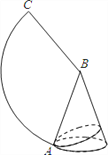
【答案】（1）∠ABC=120°；（2）这根绳子的最短长度是.

【解析】

（1）根据勾股定理直接求出圆锥的高，再利用圆锥侧面展开图弧长与其底面周长的长度关系，求出侧面展开图中∠ABC的度数即可；

（2）首先求出BD的长，再利用勾股定理求出AD以及AC的长即可．

(1)圆锥的高=

底面圆的周长等于：2π×2=，

解得：n=120°；

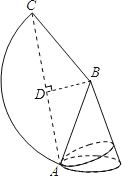
(2)连结AC,过B作BD⊥AC于D,则∠ABD=60°.

由AB=6，可求得BD=3，

∴AD═，

AC=2AD=，

即这根绳子的最短长度是.