Question

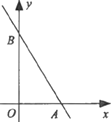
【题目】如图，抛物线与x轴交于点A，B，若点B的坐标为.

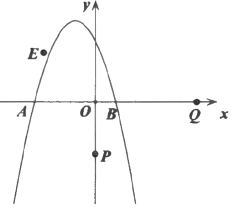
(1)求抛物线的解析式及顶点坐标；

(2)若是轴上一点，，将点Q绕着点P逆时针方向旋转90得到点E.

①用含t的式子表示点的坐标；

②当点E恰好在该抛物线上时，求t的值.

Answer 1

【答案】(1) y＝﹣x2﹣2x+3，顶点坐标为（﹣1，4）；(2) ①E的坐标为（t，5+t）；②t＝﹣2

【解析】

（1）把点B的坐标代入二次函数解析式，求出b，利用配方法求出抛物线的顶点坐标；
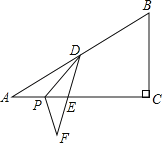
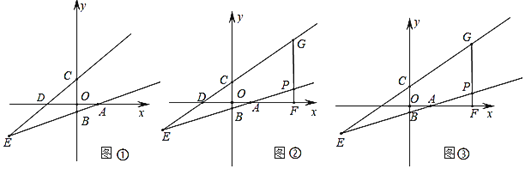
（2）①作EH⊥y轴于H，证明△EPH≌△PQO，关键全等三角形的性质得到PH=OQ=5，EH=OP=t，得到点E的坐标；
②把点E的坐标代入二次函数解析式，计算得到答案．

解：（1）∵抛物线y＝﹣x2+bx+3与x轴交于点B，点B的坐标为（1，0）．

∴﹣12+b+3＝0，

解得，b＝﹣2，

抛物线的解析式为：y＝﹣x2﹣2x+3，

y＝﹣x2﹣2x+3＝﹣（x+1）2+4，

∴抛物线的顶点坐标为（﹣1，4）；

（2）①作EH⊥y轴于H，

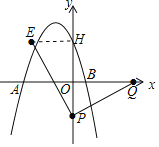
由旋转的性质可知，PE＝PQ，∠EPQ＝90°，

∴∠EPH+∠HPQ＝90°，

∵∠POQ＝90°，

∴∠OPQ+∠OQP＝90°，

∴∠EPH＝∠PQO，

在△EPH和△PQO中，

，

∴△EPH≌△PQO（AAS），

∴PH＝OQ＝5，EH＝OP＝t，

∴OH＝PH﹣OP＝5+t，

则点E的坐标为（t，5+t）；

②当点E恰好在该抛物线上时，﹣t2﹣2t+3＝5+t，

解得，t1＝﹣2，t2＝﹣1

∵t＜﹣1，

∴t＝﹣2．