Question

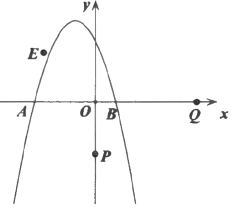
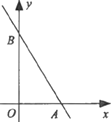
【题目】如图，在平面直角坐标系xOy中，直线与x轴，y轴分别交于点A，B，Q为内部一点，则的最小值等于( )

A.B.C.D.

Answer 1

【答案】D

【解析】

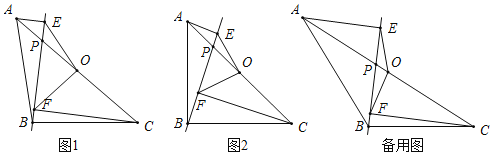
根据题意将ΔAOQ绕点A逆时针旋转60°得到ΔA0Q，连接QQ，OQ，BQ，然后根据y=-x+可得A，B两点坐标，再根据旋转的性质得出ΔAOO，ΔAQQ都是等边三角形，当A、Q、Q、0四点共线时，AQ+OQ+BQ的值最小，最后利用勾股定理求出A0的值，即AQ+OQ+BQ的值最小。

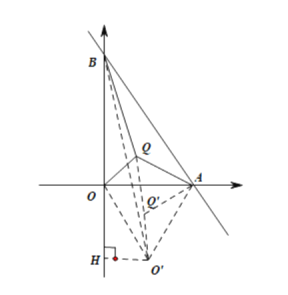
如图，将ΔAOQ绕点A逆时针旋转60°得到ΔA0Q，连接QQ，OQ，BQ，

由y=-x+可得A(1，0)，B(0，)，∴AO=1，BO=，

由旋转性质可得ΔAOO，ΔAQQ都是等边三角形，

∴QQ=AQ，OQ=OQ

当A、Q、Q、0四点共线时，AQ+OQ+BQ的值最小，即为AO的长，

∵ΔAQQ都是等边三角形，AO=1

∴O()

∴OH=，OH=

∴BH=BO+OH=

∴A0==

∴AQ+OQ+BQ的最小值是.

故答案为：D.