Question

如图, AD为△ABC的中线，BE为△ABD的中线．
（1）∠ABE=15°，∠BAD=36°，求∠BED的度数；
（2） 作出△BED中DE边上的高，垂足为H；
（3） 若△ABC面积为20,过点C作CF//AD交BA的延长线于点F，求△BCF的面积.（友情提示：两条平行线间的距离处处相等.）

Answer 1

（1）∠BED=55°；
（2）图形见解析；
（3）S_△BCF =40．

试题分析：（1）根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解；
（2）根据三角形高线的定义，过点E作BD边上的垂线段即可；
（3）利用构造三角形，寻求面积之间的关系即可．
试题解析：（1）∵∠ABE=15°，∠BAD=40°，
∴∠BED=∠ABE+∠BAD=15°+40°=55°；
（2）如图，EH即为△BED边BD上的高线；

H

（3）连接DF，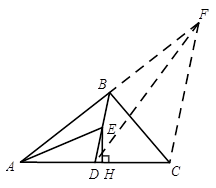

∵ AD∥CF，
∴S_△AFC =S_△DFC．
而S_△DFC =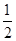S_△BCF，
∴S_△AFC =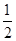S_△BCF．
∴S_△AFC =S_△ABC =20，
∴S_△BCF =40．