题目内容
【题目】如图，直线L： 
与x轴、y轴分别交于A、B两点，在y轴上有一点C（0，4），动点M从A点以每秒1个单位的速度沿x轴向左移动．
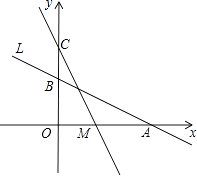
（1）求A、B两点的坐标；
（2）求△COM的面积S与M的移动时间t之间的函数关系式；
（3）当t为何值时△COM≌△AOB，并求此时M点的坐标．
【答案】
（1）
解：对于直线AB： 
，
当x=0时，y=2；当y=0时，x=4，
则A、B两点的坐标分别为A（4，0）、B（0，2）
（2）
解：∵C（0，4），A（4，0）
∴OC=OA=4，
当0≤t≤4时，OM=OA﹣AM=4﹣t，S△OCM= 
×4×（4﹣t）=8﹣2t；
当t＞4时，OM=AM﹣OA=t﹣4，S△OCM= ×4×（t﹣4）=2t﹣8
（3）
解：分为两种情况：①当M在OA上时，OB=OM=2，△COM≌△AOB．
∴AM=OA﹣OM=4﹣2=2
∴动点M从A点以每秒1个单位的速度沿x轴向左移动2个单位，所需要的时间是2秒钟；
M（2，0），
②当M在AO的延长线上时，OM=OB=2，
则M（﹣2，0），此时所需要的时间t=[4﹣（﹣2）]/1=6秒，
即M点的坐标是（2，0）或（﹣2，0）
【解析】（1）由直线L的函数解析式，令y=0求A点坐标，x=0求B点坐标；（2）由面积公式S= 
求出S与t之间的函数关系式；（3）若△COM≌△AOB，OM=OB，则t时间内移动了AM，可算出t值，并得到M点坐标．
【考点精析】根据题目的已知条件，利用一次函数的图象和性质的相关知识可以得到问题的答案，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远．
