题目内容
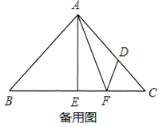
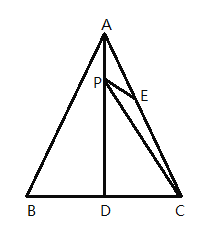
【题目】如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠CPE的度数是（ ）
A.30°B.45°C.60°D.90°
【答案】C
【解析】
连接BE，则BE的长度即为PE与PC和的最小值．再利用等边三角形的性质可得∠PBC=∠PCB=30°，即可解决问题；
解：如连接BE，与AD交于点P，此时PE+PC最小，
∵△ABC是等边三角形，AD⊥BC，
∴PC=PB，
∴PE+PC=PB+PE=BE，
即BE就是PE+PC的最小值，
∵△ABC是等边三角形，
∴∠BCE=60°，
∵BA=BC，AE=EC，
∴BE⊥AC，
∴∠BEC=90°，
∴∠EBC=30°，
∵PB=PC，
∴∠PCB=∠PBC=30°，
∴∠CPE=∠PBC+∠PCB=60°，
故选：C．
练习册系列答案
相关题目
【题目】学校组织学生到距离学校5
的县科技馆去参观，学生小明因事没能乘上学校的班车，于是准备在校门口乘出租车去县科技馆，出租车收费标准如下：
里程 | 收费/元 |
3 | 8.00 |
3 | 2.00 |
（1）出租车行驶的里程为
（
，
为整数），请用的代数式表示车费
元；
（2）小明身上仅有14元钱，够不够支付乘出租车到科技馆的车费？请说明理由．
