题目内容
【题目】如图，矩形ABCD中，对角线AC、BD相交于点O，点P是线段AD上一动点（不与与点D重合），PO的延长线交BC于Q点．
（1）求证：四边形PBQD为平行四边形．
（2）若AB＝6cm，AD＝8cm，P从点A出发．以1cm/秒的速度向点D匀速运动．设点P运动时间为t秒，问四边形PBQD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
【答案】（1）详见解析；（2）点P运动时间为
秒时，四边形PBQD是菱形．
【解析】
（1）依据矩形的性质和平行线的性质，通过全等三角形的判定定理判定△POD≌△QOB，所以OP=OQ，则四边形PBQD的对角线互相平分，故四边形PBQD为平行四边形．
（2）点P从点A出发运动t秒时，AP=tcm，PD=（4-t）cm．当四边形PBQD是菱形时，PB=PD=（4-t）cm．在直角△ABP中，根据勾股定理得AP2+AB2=PB2，即t2+32=（4-t）2，由此可以求得t的值．
（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠PDO＝∠QBO，
在△POD和△QOB中，
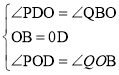
∴△POD≌△QOB（ASA），
∴OP＝OQ；
又∵OB＝OD
∴四边形PBQD为平行四边形；
（2）答：能成为菱形；
证明：t秒后AP＝t，PD＝8﹣t，
若四边形PBQD是菱形，
∴PD＝BP＝8﹣t，
∵四边形ABCD是矩形，
∴∠A＝90°，
在Rt△ABP中，由勾股定理得：AB2+AP2＝BP2，
即62+t2＝（8﹣t）2，
解得：t＝．
即点P运动时间为秒时，四边形PBQD是菱形．
练习册系列答案
相关题目
