题目内容
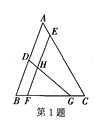
【题目】如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
(1)旋转中心;
(2)旋转角度数;
(3)图中经过旋转后能重合的三角形共有几对?若A、O、C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度;
(5)若∠A=15°,则求当A、C、B在同一条线上时的旋转角度.

【答案】(1)旋转中心是点O;
(2旋转角度数是60°;
(3)△BOE与△COF不一定重合,结论不一定成立,理由见解析;
(4)旋转角度为:90°,
(5)旋转角度为120°.
【解析】试题分析:(1) △AOB与△COD是能够重合的图形,根据旋转的性质,即可求解,
(2)根据旋转的性质,得出旋转角的度数,
(3)根据旋转的性质得出能够重合的三角形,
(4)当△BOC为等腰三角形时,所以∠BOC=∠AOD=90°,根据旋转的性质,即可解答,
(5)根据旋转的性质即可解答.
试题解析:
(1)∵△AOB与△COD是能够重合的图形,
∴旋转中心是点O,
(2)根据题意得:旋转角是∠AOD或∠BOC,
∴旋转角度数是60°,
(3)经过旋转后能重合的三角形有△AOB与△DOC,△AOE与△DOF,△BOE与△COF共三对,
若A,O,C三点不共线,△AOE与△DOF,△BOE与△COF不一定重合,结论不一定成立,
∵若A,O,C三点不共线,∠DOB≠60°,
∴∠AOD=∠BOC=60°≠∠DOB,
∴△BOE与△COF不一定重合,结论不一定成立,
(4)∵△BOC为等腰直角三角形,
∴∠BOC=∠AOD=90°,
∴旋转角度为:90°,
(5)∵180°﹣∠BOC=180°﹣60°=120°,
∴旋转角度为120°.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
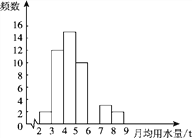
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.