题目内容
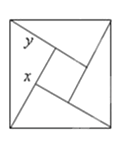
【题目】图①是一个长为 a,宽为 b 的长方形.现将相等的长方形若干,拼接组成如下图 形.
(1)将图①中所得的四块长为 a,宽为 b 的小长方形拼成一个正方形(如图②).请利用 图②中阴影部分面积的不同表示方法,直接写出代数式(a+b)2、(a﹣b)2、ab 之间的等量关系是 ;
(2)根据(2)题中的等量关系,解决如下问题:已知 m+n=6,mn=5,则 m﹣n= ;
(3)将图①中的长方形和图③中的两个边长分别为 a、b 的正方形若干个,拼成如图④的长方形,则图④中的长方形的面积可以用两种不同的方法表示,则关系式 .

【答案】(1)(a﹣b)2=(a+b)2﹣4ab;(2)±4;(3)(2a+b)(a+b)=2a2+3ab+b2.
【解析】
(1)利用大正方形的面积减4个小长方形的面积等于小正方形的面积列式即可;
(2)利用公式(m﹣n)2=(m+n)2﹣4mn求解即可;
(3)根据大长方形面积等于长乘以宽或2个边长为a的正方形、1个边长为b的正方形加上3个长为a、宽为b的小长方形面积和列式可得.
解:(1)(a﹣b)2=(a+b)2﹣4ab.
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(2)∵m+n=6,mn=5,
∴(m﹣n)2=(m+n)2﹣4mn=36﹣20=16,
∴m﹣n=±4
故答案为:±4;
(3)根据大长方形面积等于长乘以宽有:(2a+b)(a+b),
或2个边长为a的正方形、1个边长为b的正方形加上3个长为a、宽为b的小长方形面积和有:2a2+3ab+b2,
故可得:(2a+b)(a+b)=2a2+3ab+b2.
故答案为:(2a+b)(a+b)=2a2+3ab+b2.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】甲、乙两名选手在同等条件下进行射击对抗赛,他们各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | ||||
乙 |

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?