��Ŀ����
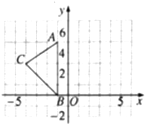
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��A��a��0����B(b��O)�ֱ���x���������y���������ϣ���![]() ����P��ԭ�������ÿ��2����λ���ȵ��ٶ���x�������᷽���˶���
����P��ԭ�������ÿ��2����λ���ȵ��ٶ���x�������᷽���˶���
(1)���A��B�����ꣻ
(2)����PB����������ABP�����Ϊs����P���˶�ʱ��Ϊt�����ú�t��ʽ�ӱ�ʾs����ֱ��д��t��ȡֵ��Χ��
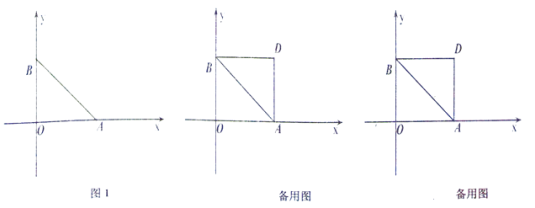
(3)��(2)�������£����߶�OB��x��������ƽ�ƣ�ʹ��O���A�غϣ���B�Ķ�Ӧ��Ϊ��D������BD�����߶�PB��x��������ƽ�ƣ�ʹ��B���D�غϣ���P�Ķ�Ӧ��Ϊ��Q��ȡDQ���е�H���Ƿ����t��ֵ��ʹ������ABP���������������ADH������������ڣ����t��ֵ���������ڣ���˵������.
���𰸡���1��A��4��0����B��0��3������2���ٵ�P���߶�OA��ʱ��S��![]() ��
��![]() �����ڵ�P���߶�OA���ӳ�����ʱ��S��
�����ڵ�P���߶�OA���ӳ�����ʱ��S��![]() ��
��![]() ������3���ٵ�P���߶�OA��ʱ��
������3���ٵ�P���߶�OA��ʱ�� ![]() ���ڵ�P���߶�OA���ӳ�����ʱ��t=4
���ڵ�P���߶�OA���ӳ�����ʱ��t=4
����������1�����ݷǸ��������ʣ������Ԫһ�η��������õ�a��b��ֵ���ɣ�
��2��������ã�OP=![]() ��������������ٵ�P���߶�OA��ʱ���ڵ�P���߶�OA���ӳ�����ʱ����⼴�ɣ�
��������������ٵ�P���߶�OA��ʱ���ڵ�P���߶�OA���ӳ�����ʱ����⼴�ɣ�
��3��������ã�BD=OA��BD=PQ��OB=AD �������е�����ʣ��õ�DH=HQ������A��AM��DQ�ڵ�M���õ�S��AHQ= S��ADH��Ȼ���Ϊ�ٵ�P���߶�OA��ʱ���ڵ�P���߶�OA���ӳ�����ʱ���������ε������⼴��.
��1���⣺��![]()
��![]() ��
��
���![]() ��
��
��A��4��0����B��0��3����
��2��������ã�OP=![]() ��
��
�ٵ�P���߶�OA��ʱ��AP=4-![]()
��S=![]() ��AP��OB=
��AP��OB=![]() ����4-
����4-![]() ����3=
����3=![]() ��
��![]() ����
����
�ڵ�P���߶�OA���ӳ�����ʱ��AP=![]() -4
-4
��S=![]() ��AP��OB=
��AP��OB=![]() ����
����![]() -4����3=
-4����3=![]() ��
��![]() ����
����
��3��������ã�BD=OA��BD=PQ��OB=AD
��OA=PQ
�ߵ�HΪDQ���е�
��DH=HQ
����A��AM��DQ�ڵ�M
��S��AHQ=![]() HQ��AM��S��ADH=
HQ��AM��S��ADH=![]() DH��AM
DH��AM
��S��AHQ= S��ADH��

�ٵ�P���߶�OA��ʱ��
��OA-PA=PQ-PA
�� OP=AQ
��OB��AD
���DAQ=90��
��S��ADQ=S��OBP
��S��ADH=![]() S��ADQ=
S��ADQ=![]() S��BOP��
S��BOP��
�� ![]() =
=![]() ��
��![]() ��3��
��3��![]()
![]() ��
��
�ڵ�P���߶�OA���ӳ�����ʱ
��OA+PA=PQ+PA
�� OP=AQ
��OB��AD
���DAQ=90��
��S��ADQ=S��OBP
��S��ADH=![]() S��ADQ=
S��ADQ=![]() S��BOP
S��BOP
�� ![]() =
=![]() ��
��![]() ��3��
��3��![]()
t![]() .
.

 ��У����ϵ�д�
��У����ϵ�д�