Question

【题目】如图所示，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边（x＞y），下列四个说法：①x2+y2=49，②x-y=2，③2xy+4=49，④x+y=9．其中说法正确的结论有______________

Answer 1

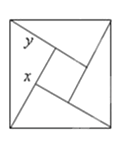
【答案】①②③

【解析】

根据大正方形的面积和勾股定理可判断①正确；利用小正方形的边长与直角三角形的边长之间的关系可判断②正确；根据四个三角形的面积+小正方形的面积=大正方形的面积可判断③正确；根据①③可知x+y=即可判断④不正确.

①大正方形的面积是49，则其边长是7，显然，利用勾股定理可得x2+y2=49，故选项①正确；

②小正方形的面积是4，则其边长是2，根据图可发现y+2=x，即x-y=2，故选项②正确；

③根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积，即4×xy+4=49，化简得2xy+4=49，故选项③正确；

④因为（x+y）2=x2+y2+2xy=49+45=94，所以x+y=，故此选项不正确．

故答案为：①②③.