Question

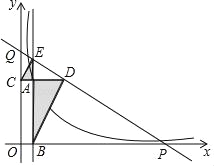
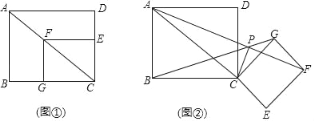
【题目】如图①，四边形ABCD与四边形CEFG都是矩形，点E，G分别在边CD，CB上，点F在AC上，AB＝3，BC＝4

（1）求的值；

（2）把矩形CEFG绕点C顺时针旋转到图②的位置，P为AF，BG的交点，连接CP

（Ⅰ）求的值；

（Ⅱ）判断CP与AF的位置关系，并说明理由．

Answer 1

【答案】（1）；（2）（Ⅰ）；（Ⅱ）CP⊥AF，理由：见解析.

【解析】

(1)根据矩形的性质得到∠B＝90°，根据勾股定理得到AC＝5，根据相似三角形的性质即可得到结论；

(2)(Ⅰ)连接CF，根据旋转的性质得到∠BCG＝∠ACF，根据相似三角形的判定和性质定理得到结论；

(Ⅱ)根据相似三角形的性质得到∠BGC＝∠AFC，推出点C，F，G，P四点共圆，根据圆周角定理得到∠CPF＝∠CGF＝90°，于是得到结论．

(1)∵四边形ABCD是矩形，

∴∠B＝90°，

∵AB＝3，BC＝4，

∴AC＝5，

∴，

∵四边形CEFG是矩形，

∴∠FGC＝90°，

∴GF∥AB，

∴△CGF∽△CBA，

∴，

∵FG∥AB，

∴；

(2)(Ⅰ)连接CF，

∵把矩形CEFG绕点C顺时针旋转到图②的位置，

∴∠BCG＝∠ACF，

∵，

∴△BCG∽△ACF，

∴；

(Ⅱ)CP⊥AF，

理由：∵△BCG∽△ACF，

∴∠BGC＝∠AFC，

∴点C，F，G，P四点共圆，

∴∠CPF＝∠CGF＝90°，

∴CP⊥AF．