Question

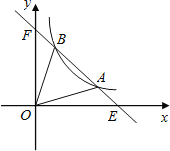
【题目】如图，直线与双曲线交于A、B两点，与x轴、y轴分别交于E、F两点，连接OA、OB，若 ，则______．

Answer 1

【答案】

【解析】

试题根据直线解析式求出点E、F的坐标，过点O作OM⊥AB于点M，设A（x1，y1）、B（x2，y2），联立两函数解析式求解可得y1=x2，y2=x1，从而判断出点A、B关于OM对称，并求出点A的坐标，然后代入双曲线解析式计算即可得解．

解：令y=0，则﹣x+b=0，

解得x=b，

令x=0，则y=b，

所以，点E（b，0）、F（0，b），

所以，OE=OF，

过点O作OM⊥AB于点M，则ME=MF，

设点A（x1，y1）、B（x2，y2），

联立，

消掉y得，x2﹣bx+1=0，

根据根与系数的关系，x1x2=1，

所以y1y2=1，

所以y1=x2，y2=x1，

所以OA=OB，

所以AM=BM（等腰三角形三线合一），

∵S△AOB=S△OBF+S△OAE，

∴FB=BM=AM=AE，

所以点A（b，b），

∵点A在双曲线y=上，

∴b×b=1，

解得b=．

故答案为：．