题目内容
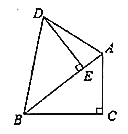
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点H,点D在AH上,且
于点H,点D在AH上,且![]() ,连接BD.
,连接BD.
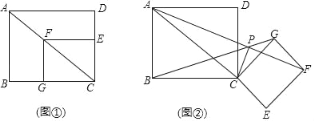
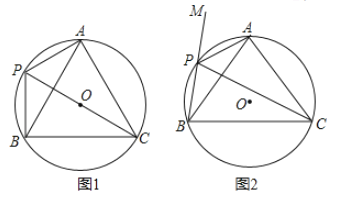
![]() 如图1,将
如图1,将![]() 绕点H旋转,得到
绕点H旋转,得到![]() 点B、D分别与点E、F对应
点B、D分别与点E、F对应![]() ,连接AE,当点F落在AC上时
,连接AE,当点F落在AC上时![]() 不与C重合
不与C重合![]() ,求AE的长;
,求AE的长;
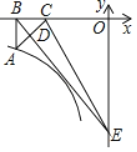
![]() 如图2,
如图2,![]() 是由
是由![]() 绕点H逆时针旋转
绕点H逆时针旋转![]() 得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.

【答案】(1)证明见解析;(2)(I)AE=![]() ;(II)
;(II)![]() .
.
【解析】
(1)先根据tanC=3,求出AH=3,CH=1,然后根据△EHA∽△FHC,得到,HP=3AP,AE=2AP,最后用勾股定理即可;
(2)先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可.
,然后判断出△AQC∽△GQH,用相似比即可.
(1)如图,
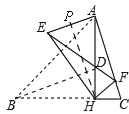
在Rt△AHC中,
∵tanC=3,
∴![]() =3,
=3,
设CH=x,
∴BH=AH=3x,
∵BC=4,
∴3x+x=4,
∴x=1,
∴AH=3,CH=1,
由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHF+∠AHF=∠AHC+∠AHF,
∴∠EHA=∠FHC,![]() =1,
=1,
∴△EHA∽△FHC,
∴∠EAH=∠C,
∴tan∠EAH=tanC=3,
过点H作HP⊥AE,
∴HP=3AP,AE=2AP,
在Rt△AHP中,AP2+HP2=AH2,
∴AP2+(3AP)2=9,
∴AP=![]() ,
,
∴AE=![]() ;
;
(2)如图1,
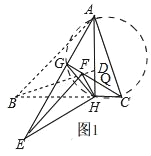
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQH,
∴△AQC∽△GQH,
∴![]() ,
,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴EF=BD,
由(1)知,BD=AC,
∴EF=AC
∴![]() =2,
=2,
即:EF=2HG,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案