题目内容
【题目】如图,直径为10的半圆O,tan∠DBC= ![]() ,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.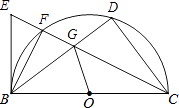
(1)求证:BE为⊙O切线;
(2)求证:BG2=FGCE;
(3)求OG的值.
【答案】
(1)证明:由同弧所对的圆周角相等得∠FBD=∠DCF,
又∵CF平分∠BCD,
∴∠BCF=∠DCF,
已知∠EBF=∠GBF,
∴∠EBF=∠∠BCF,
∵BC为⊙O直径,
∴∠BFC=90°,
∴∠FBC+∠FCB=90°,
∴∠FBC+∠EBF=90°,
∴BE⊥BC,
∴BE为⊙O切线
(2)证明:由(1)知∠BFC=∠EBC=90°,∠EBF=∠ECB,
∴△BEF∽△CEB,
∴BE2=EFCE,
又∠EBF=∠GBF,BF⊥EG,
∴∠BFE=∠BFG=90°,
在△BEF与△BGF中, 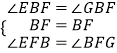 ,
,
∴△BEF≌△BGF,
∴BE=BG,EF=FG,
∴BG2=FGCE
(3)解:如图,过G作GH⊥BC于H, 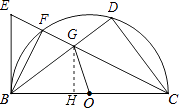
∵CF平分∠BCD,
∴GH=GD,
∵tan∠DBC= ![]() ,
,
∴sin∠DBC= ![]() ,
,
∵BC=10,
∴BD=8,BG=BD﹣GD=8﹣GD,
∴ ![]() =
= ![]() ,
,
∴GD=GH=3,BG=5,BH=4,
∵BC=10,∴OH=OB﹣BH=1,
在Rt△OGH中,由勾股定理得OG= ![]() .
.
【解析】(1)首先依据圆周角定理得到∠FBD=∠DCF,结合角平分线的定义可证明∠EBF=∠∠BCF,故此可得到BE⊥BC;
(2)由(1)知∠BFC=∠EBC=90°,∠EBF=∠ECB,然后依据相似三角形的性质得到BE2=EFCE,得到∠BFE=∠BFG=90°,故此可证明△BEF≌△BGF,根据全等三角形的性质得到BE=BG,EF=FG,最后,通过等量代换可得到问题的答案;
(3)过G作GH⊥BC于H,首先依据角平分线的性质得到GH=GD,接下来,在依据三角函数的定义得到![]() =
=![]() =
=![]() 从而可求得DG的长,最后,在依据勾股定理求解即可.
从而可求得DG的长,最后,在依据勾股定理求解即可.
【考点精析】利用切线的判定定理和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】某体育老师测量了自己任教的甲、乙两班男生的身高,并制作了如下不完整的统计图表
身高分组 | 频数 | 频率 |
152≤ x<155 | 3 | 0.06 |
155≤ x<158 | 7 | 0.14 |
158≤ x<161 | m | 0.28 |
161≤ x<164 | 13 | n |
164≤ x<167 | 9 | 0.18 |
167≤ x<170 | 3 | 0.06 |
170≤ x<173 | 1 | 0.02 |

根据以上统计图表完成下列问题:
(1)统计表中m=____,n=____;并将频数分布直方图补充完整;
(2)在这次测量中两班男生身高的中位数在什么范围内?