题目内容
【题目】已知抛物线y1=ax2+bx﹣4（a≠0）与x轴交于点A（﹣1，0）和点B（4，0）．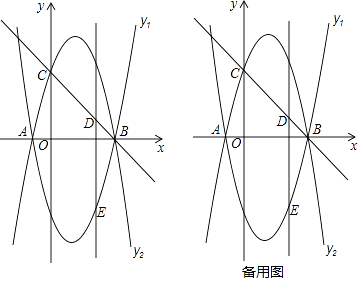
（1）求抛物线y1的函数解析式；
（2）如图①，将抛物线y1沿x轴翻折得到抛物线y2 ， 抛物线y2与y轴交于点C，点D是线段BC上的一个动点，过点D作DE∥y轴交抛物线y1于点E，求线段DE的长度的最大值；
（3）在（2）的条件下，当线段DE处于长度最大值位置时，作线段BC的垂直平分线交DE于点F，垂足为H，点P是抛物线y2上一动点，⊙P与直线BC相切，且S⊙P：S△DFH=2π，求满足条件的所有点P的坐标．
【答案】
（1）解：将点A（﹣1，0）和点B（4，0）代入y1=ax2+bx﹣4得：a=1，b=﹣3，
∴抛物线y1的函数解析式为：y1=x2﹣3x﹣4；
（2）解：由对称性可知，抛物线y2的函数解析式为：y2=﹣x2+3x+4，
∴C（0，4），设直线BC的解析式为：y=kx+q，
把B（4，0），C（0，4）代入得，k=﹣1，q=4，
∴直线BC的解析式为：y=﹣x+4，
设D（m，﹣m+4），E（m，m2﹣3m﹣4），其中0≤m≤4，
∴DE=﹣m+4﹣（m2﹣3m﹣4）=﹣（m﹣1）2+9，
∵0≤m≤4，∴当m=1时，DEmax=9；
此时，D（1，3），E（1，﹣6）；
（3）解：由题意可知，△BOC是等腰直角三角形，
∴线段BC的垂直平分线为：y=x，
由（2）知，直线DE的解析式为：x=1，
∴F（1，1），
∵H是BC的中点，
∴H（2，2），
∴DH= 
，FH= ，
∴S△DFH=1，
设⊙P的半径为r，
∵S⊙P：S△DFH=2π，
∴r= ,
∵⊙P与直线BC相切，
∴点P在与直线BC平行且距离为 的直线上，
∴点P在直线y=﹣x+2或y=﹣x+6的直线上，
∵点P在抛物线y2=﹣x2+3x+4上，
∴﹣x+2=﹣x2+3x+4，
解得：x1=2+ 
，x2=2﹣ ，
﹣x+6=﹣x2+3x+4，
解得：x3=2+ ，x4=2﹣ ，
∴符合条件的点P坐标有4个，分别是（2+ ，﹣ ），（2﹣ ， ），（2+ ，4﹣ ），（2﹣ ，4+ ）．
【解析】（1）（1）把A（﹣1，0）和点B（4，0）坐标代入抛物线解析式，利用待定系数法即可求出；（2）关于x轴翻折后的解析式可套用点关于x轴对称坐标变换方法即x不变，y变为其相反数-y ,-y=x2﹣3x﹣4,即y2=﹣x2+3x+4；竖直线段的最值问题可以化归为函数最值问题，须构建以动点D的横坐标m为自变量，DE长为因变量的函数，竖直线段等于上、下两端点的纵坐标之差来表示，二次函数最值问题可用配方法解决；（3）利用互垂直线的斜率积=-1求出BC的垂直平分线的解析式，由S⊙P：S△DFH=2π，得r= ,，由⊙P与直线BC相切，可知点P在与直线BC平行且距离为 的直线上，由点P在直线y=﹣x+2或y=﹣x+6的直线上，点P在抛物线y2=﹣x2+3x+4上，联立解析式﹣x+2=﹣x2+3x+4和﹣x+6=﹣x2+3x+4，分别解方程即可.
