题目内容
【题目】以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1),一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】∵矩形的两条对称轴相交于对角线的交点处,即坐标原点是对角线的交点,
∴点C和点A关于原点对称,
∴点C的坐标为(-2,1),
要把抛物线上的一点由点A移到点C,就需要将抛物线向左移动4个单位,再向下移动2个单位,
∴移动后,抛物线的解析式为: ![]() ,即
,即 ![]() .
.
所以答案是:A.
【考点精析】本题主要考查了矩形的性质和坐标与图形变化-平移的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能正确解答此题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
【题目】如图所示的是用棋子成的T字形图案:
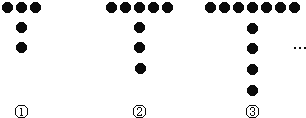
(1)填写下表:
图案序号 | ① | ② | ③ | ④ | …… | ⑧ |
每个图案中棋子的个数 | 5 | 8 | …… |
(2)第![]() 个“T“字形图案中棋子的个数为多少 (用含
个“T“字形图案中棋子的个数为多少 (用含![]() 的代数式表示);
的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.