题目内容
【题目】阅读下面的解题过程,解答后面的问题:
如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 点的坐标;
点的坐标;
解:分别过![]() ,
,![]() 做
做![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 做
做![]() 轴的平行线,两组平行线的交点如图
轴的平行线,两组平行线的交点如图![]() 所示,设
所示,设![]() ,则
,则![]() ,
,![]() ,
,![]()
由图![]() 可知:
可知:
![]()
![]()
![]() 线段
线段![]() 的中点
的中点![]() 的坐标为
的坐标为![]()
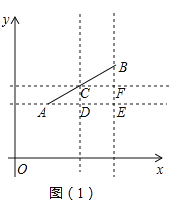
(应用新知)
利用你阅读获得的新知解答下面的问题:
(1)已知![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为
(2)平行四边形![]() 中,点
中,点![]() ,
,![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,利用中点坐标公式求点
,利用中点坐标公式求点![]() 的坐标。
的坐标。
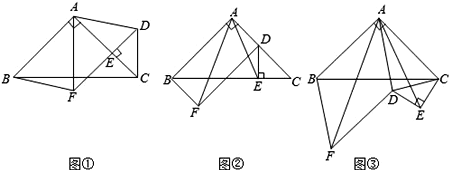
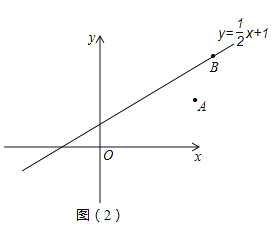
(3)如图![]() ,点
,点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() ,
,![]() 在
在![]() 轴上,
轴上,![]() 在函数
在函数![]() 的图象上 ,以
的图象上 ,以![]() ,
,![]() ,
,![]() ,
,![]() 四个点为顶点,且以
四个点为顶点,且以![]() 为一边构成平行四边形,直接写出所有满足条件的
为一边构成平行四边形,直接写出所有满足条件的![]() 点坐标。
点坐标。
【答案】(1)线段![]() 的中点坐标是
的中点坐标是![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)符合条件的
;(3)符合条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
【解析】
(1)直接套用中点坐标公式,即可得出中点坐标;
(2)根据AC、BD的中点重合,可得出![]() ,代入数据可得出点D的坐标;
,代入数据可得出点D的坐标;
(3)当AB为该平行四边形一边时,此时CD∥AB,分别求出以AD、BC为对角线时,以AC、BD为对角线的情况可得出点D坐标.
解:(1)AB中点坐标为![]() ,即AB的中点坐标是:(1,1);
,即AB的中点坐标是:(1,1);
(2)根据平行四边形的性质:对角线互相平分,可知![]() 、
、![]() 的中点重合,
的中点重合,
由中点坐标公式可得:![]() ,
,![]()
代入数据,得:![]() ,
,![]()
解得:![]() ,
,![]() ,所以点
,所以点![]() 的坐标为
的坐标为![]() ;
;
(3)当![]() 为该平行四边形一边时,则
为该平行四边形一边时,则![]() ,对角线为
,对角线为![]() 、
、![]() 或
或![]() 、
、![]() ;
;
故可得:![]() ,
,![]() 或
或![]() ,
,![]() .
.
故可得![]() 或
或![]() ,
,
![]() ,
,
![]()
![]() 或
或![]()
代入到![]() 中,可得
中,可得![]() 或
或![]() .
.
综上,符合条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.

【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米).
表示立方米).
每月用水量 | 单价 |
不超过 | 2元/ |
超出 | 4元/ |
超出 | 8元/ |
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水![]() ,则应收水费_________.元
,则应收水费_________.元
(2)若该户居民3月份用水![]() (其中
(其中![]() ),则应收水费多少元(用含a的代数式表示,并简化).
),则应收水费多少元(用含a的代数式表示,并简化).
(3)若该户居民4,5两个月共用水![]() (5月份用水量超过了4月份),设4月份,用水
(5月份用水量超过了4月份),设4月份,用水![]() ,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).