题目内容
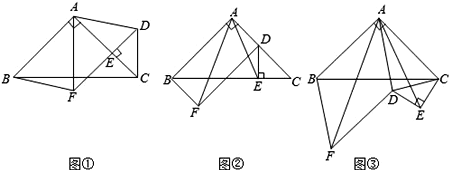
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论.
![]()
【答案】(1)AF=![]() AE;
AE;
(2)AF=![]() AE,证明见解析.
AE,证明见解析.
【解析】解:(1)如图①中,∵四边形ABFD是平行四边形,
∴AB=DF,∵AB=AC,∴AC=DF,∵DE=EC,∴AE=EF,
∵∠DEC=∠AEF=90°,∴△AEF是等腰直角三角形, ∴AF=![]() AE.
AE.
(2)如图②中,连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,∴AB∥DF,
∴∠DKE=∠ABC=45°,∴EKF=180°﹣∠DKE=135°,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,∴∠EKF=∠ADE,
∵∠DKC=∠C,∴DK=DC,∵DF=AB=AC,∴KF=AD, 在△EKF和△EDA中,
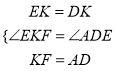 ,
,
∴△EKF≌△EDA, ∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,∴△AEF是等腰直角三角形,∴AF=![]() AE.
AE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目