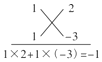题目内容
【题目】已知二次函数
的图象与
轴交于点
、
，且
，与
轴的正半轴的交点在
的下方．下列结论：①
；②
；③
；④
；⑤
．其中正确结论的个数是________个．
【答案】3
【解析】
本题依据二次函数图象的画法画出大致图象，进一步利用方程根与系数的关系等知识和数形结合能力仔细分析即可解．
如图：
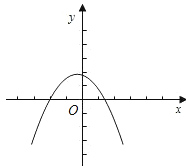
①由图象开口向下知a＜0，由y=ax2+bx+c与x轴的另一个交点坐标为（x1，0 ），且1＜x1＜2，则该抛物线的对称轴为x=﹣
=
＞﹣
，即
＜1，由a＜0，两边都乘以a得：b＞a．
∵a＜0，对称轴x=﹣＜0，∴b＜0；此项错误；
②因为1＜x1＜2，当x=1时，对应图象上的点在x轴上方，所以a+b+c＞0；所以此项错误；
③由y=ax2+bx+c与x轴的交点坐标为（﹣2，0）得：
a×（﹣2）2+b×（﹣2 ）+c=0，即4a﹣2b+c=0，所以③正确；
④由4a﹣2b+c=0得2a﹣b=﹣
，而0＜c＜2，∴－1＜2a﹣b＜0，所以结论正确．
⑤由一元二次方程根与系数的关系知x1x2=
＜﹣2，结合a＜0得2a+c＞0，所以结论正确．
故答案为：正确结论的个数是3个．
故答案为：3．
练习册系列答案
相关题目
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |
请你结合图表中所提供的信息，回答下列问题：
（1）表中m= ，n= ；
（2）请补全频数分布直方图；
（3）在扇形统计图中，
这一组所占圆心角的度数为 度；
（4）如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．
