Question

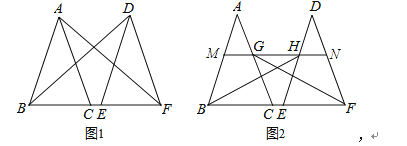
【题目】已知△ABC，AB=AC，将△ABC沿BC方向平移得到△DEF．

（1）如图1，连接BD，AF，则BD AF（填“＞”、“＜”或“=”）；
（2）如图2，M为AB边上一点，过M作BC的平行线MN分别交边AC，DE，DF于点G，H，N，连接BH，GF，求证：BH=GF．

Answer 1

【答案】
（1）=
（2）

证明：如图：

MN∥BF，

△AMG∽△ABC，△DHN∽△DEF，

=，=，

∴MG=HN，MB=NF．

在△BMH和△FNG中，

，

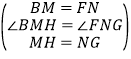△BMH≌△FNG（SAS），

∴BH=FG．

【解析】（1）根据等腰三角形的性质，可得∠ABC与∠ACB的关系，根据平移的性质，可得AC与DF的关系，根据全等三角形的判定与性质，可得答案；
（2）根据相似三角形的判定与性质，可得GM与HN的关系，BM与FN的关系，根据全等三角形的判定与性质，可得答案．
【考点精析】本题主要考查了等腰三角形的性质和平移的性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；①经过平移之后的图形与原来的图形的对应线段平行（或在同一直线上）且相等，对应角相等，图形的形状与大小都没有发生变化；②经过平移后，对应点所连的线段平行（或在同一直线上）且相等才能正确解答此题．