题目内容
【题目】如图,△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,E在线段AC上,连接AD, BE的延长线交AD于F.
(1)猜想线段BE、AD的数量关系和位置关系:_______________(不必证明);
(2)当点E为△ABC内部一点时,使点D和点E分别在AC的两侧,其它条件不变.
①请你在图2中补全图形;
②(1)中结论成立吗?若成立,请证明;若不成立,请说明理由.

【答案】BE=AD,BE⊥AD
【解析】
(1)判定△BCE≌△ACD,运用全等三角形的性质,即可得到线段BE,AD的数量关系和位置关系;
(2)①依据点E为△ABC内部一点时,点D和点E分别在AC的两侧,其它条件不变,即可补全图形;②判定△BCE≌△ACD,运用全等三角形的性质,即可得到线段BE,AD的数量关系和位置关系.
(1)BE=AD,BE⊥AD;
(2)①如图所示:
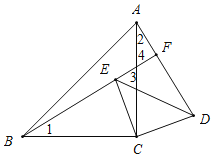
②(1)中结论仍然成立.
证明:∵△ABC和△DEC都是等腰直角三角形,∠ACB=∠DCE=90°,
∴BC=AC,EC=DC,
∵∠ACB=∠DCE=90°,
∴∠ACB=∠DCE,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
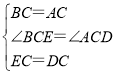 ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠1=∠2,
∵∠3=∠4,
∴∠AFB=∠ACB=90°,
∴BE⊥AD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目








