题目内容
【题目】如图,AD是Rt△ABC斜边BC上的高.
(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);
(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;
(3)在(2)的条件下,连结DEDH.求证:ED⊥HD.

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】分析:
(1)按作角的平分线的尺规作图方法作出相应的图形,并标上相应的字母即可;
(2)如图2,由已知条件易得∠1=∠2,∠1=∠3,从而可得∠2=∠3,由此即可得到FH=CH;
(3)如图3,由已知条件易证∠4=∠5,从而可得AE=AF,由FH∥CD可得△AFH∽△ADC,由此可得![]() 结合FH=CH,AE=AF可得
结合FH=CH,AE=AF可得![]() ,再证∠EAD=∠HCD,即可得到△EAD∽△HCD,从而可得∠7=∠8,结合AD⊥BC即可得到∠EDH=90°,由此即可得到DE⊥DH.
,再证∠EAD=∠HCD,即可得到△EAD∽△HCD,从而可得∠7=∠8,结合AD⊥BC即可得到∠EDH=90°,由此即可得到DE⊥DH.
详解:
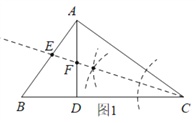
(1)如下图1所示,线段CE为所求的△ABC的角平分线;
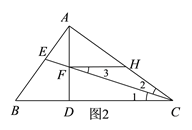
(2)FH=CH,理由如下:
如图2,∵FH∥BC,
∴∠1=∠3,
∵CE平分∠ACB,
∴∠1=∠2,
∴∠2=∠3,
∴FH=CH(等角对等边);
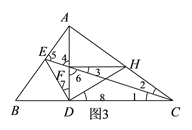
(3)如图3,∵EA⊥CA,
∴∠EAC=90°,
∴∠2+∠5=90°,
∵AD⊥DC,
∴∠ADC=90°,
∴∠1+∠6=90°,
∴∠2+∠5=∠1+∠6,
又∵∠1=∠2,
∴∠5=∠6,
∵∠6=∠4,
∴∠5=∠4,
∴AE=AF(等角对等边),
∵FH∥BC,
∴AFH∽△ADC,
∴![]() =
=![]() ,
,
∵FH=CH,
∴得![]() =
=![]() ,
,
∵∠EAD+∠DAC=90°,∠HCD+∠DAC=90°,
∴∠EAD=∠HCD,
∴△EAD∽△HCD(两边对应成比例且夹角相等的两个三角形相似),
∴∠7=∠8,
∵∠8+∠HDA=90°,
∴∠7+∠HDA=90°,即∠EDH=90°,
∴ED⊥HD