题目内容
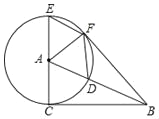
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
【答案】(1)证明见解析;(2)当∠CAB=60°时,四边形ADFE为菱形;证明见解析;
【解析】
分析(1)首先利用平行线的性质得到∠FAB=∠CAB,然后利用SAS证得两三角形全等,得出对应角相等即可;
(2)当∠CAB=60°时,四边形ADFE为菱形,根据∠CAB=60°,得到∠FAB=∠CAB=∠CAB=60°,从而得到EF=AD=AE,利用邻边相等的平行四边形是菱形进行判断四边形ADFE是菱形.
(1)证明:∵EF∥AB
∴∠FAB=∠EFA,∠CAB=∠E
∵AE=AF
∴∠EFA =∠E
∴∠FAB=∠CAB
∵AC=AF,AB=AB
∴△ABC≌△ABF
∴∠AFB=∠ACB=90°, ∴BF是⊙A的切线.
(2)当∠CAB=60°时,四边形ADFE为菱形.
理由:∵EF∥AB
∴∠E=∠CAB=60°
∵AE=AF
∴△AEF是等边三角形
∴AE=EF,
∵AE=AD
∴EF=AD
∴四边形ADFE是平行四边形
∵AE=EF
∴平行四边形ADFE为菱形.

【题目】下表中给出了变量x,与y=ax2,y=ax2+bx+c之间的部分对应值,(表格中的符号“…”表示该项数据已丢失)
x | ﹣1 | 0 | 1 |
ax2 | … | … | 1 |
ax2+bx+c | 7 | 2 | … |
(1)求抛物线y=ax2+bx+c的表达式
(2)抛物线y=ax2+bx+c的顶点为D,与y轴的交点为A,点M是抛物线对称轴上一点,直线AM交对称轴右侧的抛物线于点B,当△ADM与△BDM的面积比为2:3时,求B点坐标;
(3)在(2)的条件下,设线段BD与x轴交于点C,试写出∠BAD和∠DCO的数量关系,并说明理由.