题目内容
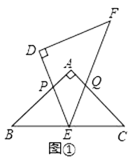
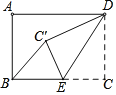
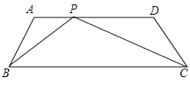
【题目】已知在梯形ABCD中,AD // BC,AD < BC,且AD = 5,AB = DC = 2,
(1)如图:P为AD上的一点,满足![]() ;
;
① ![]() ;
;
② 求AP的长
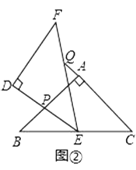
(2)如果点P在AD上移动(点P与点A、D不重合),且满足![]() ,PE交直线与BC于点E,同时交直线DC于点Q,那么
,PE交直线与BC于点E,同时交直线DC于点Q,那么
① 当点Q在线段DC的延长线上时,设AP = x,CQ = y,求y关于x的函数解析式,并写出函数的定义域;
② 当CE = 1时,写出AP的长(不必写出解题过程)
【答案】(1)① 见解析;② AP的长为1或4;(2)① y=3x-2(1 < x < 4);② AP的长为2.
【解析】
(1)①当∠BPC=∠A时,∠A+∠APB+∠ABP=180°,而∠APB+∠BPC+∠DPC=180°,因此∠ABP=∠DPC,此时三角形APB与三角形DPC相似.
②利用相似三角形的性质可得出关于AP,PD,AB,CD的比例关系式,AB,CD的值题中已经告诉,可以先用AP表示出PD,然后代入上面得出的比例关系式中求出AP的长.
(2)①与(1)的方法类似,只不过把DC换成了DQ,那么只要用DC+CQ就能表示出DQ了.然后按得出的关于AB,AP,PD,DQ的比例关系式,得出x,y的函数关系式.
②和①的方法类似,但是要多一步,要先通过平行得出三角形PDQ和CEQ相似,根据CE的长,用AP表示出PD,然后根据PD,DQ,QC,CE的比例关系用AP表示出DQ,然后按①的步骤进行求解即可.
(1)①∵ABCD是梯形,AD∥BC,AB=DC.
∴∠A=∠D
∵∠ABP+∠APB+∠A=180°,∠APB+∠DPC+∠BPC=180°,∠BPC=∠A
∴∠ABP=∠DPC,
∴△ABP∽△DPC.
②∵△ABP∽△DPC,
∴![]() ,即:
,即:![]() ,
,
解得:AP=1或AP=4.
(2)①由(1)可知:△ABP∽△DPQ
∴![]() ,即:
,即:![]() ,
,
∴y=![]() x2+
x2+![]() x2(1<x<4).
x2(1<x<4).
②当CE=1时,
∵△PDQ∽△ECQ,
∴![]() ,即
,即![]() 或
或![]() ,
,
∵y=![]() x2+
x2+![]() x2,
x2,
解得:x=2或3![]() ,
,
∴PA=2或3![]() .
.

【题目】甲、已两家商场平时以同样价格出售相同的商品,春节期间两家商场都让利酬宾,其中甲商场所有商品按![]() 折出售,乙商场对一次购物中超过200元后的价格部分打
折出售,乙商场对一次购物中超过200元后的价格部分打![]() 折. 设原价购物金额累计为
折. 设原价购物金额累计为![]() 元(
元(![]() ).
).
![]() 根据题意,填写下表: (单位:元)
根据题意,填写下表: (单位:元)
原价购物金额累计/元. | 130 | 300 | 700 | ··· |
甲商场实际购物金额/元 | 104 | 560 | ··· | |
乙商场实际购物金额/元 | 130 | 270 | ··· |
![]() 设在甲商场实际购物金额为
设在甲商场实际购物金额为![]() 元,在乙商场实际购物金额为
元,在乙商场实际购物金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
![]() 根据题意填空:
根据题意填空:
①若在同甲商场和在乙商场实际购物花费金额一样多,则在同一商场所购商品原价金额累计为______元 ;
②若在同一商场购物,商品原价购物金额累计为![]() 元,则在甲、乙.两家商场中的 商场实际购物花费金少.
元,则在甲、乙.两家商场中的 商场实际购物花费金少.
③若在同一商场实际购物金额为![]() 元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.
元,则在甲、乙两家商场中的_____商场商品原价购物累计金额多.