题目内容
如图,抛物线与x轴交于A(6,0)、B(19,0)两点,与y轴交于点C(0,8),直线CD∥x轴交抛物线于D点.动点P,Q分别从C,D两点同时出发,速度均为每秒1个单位,点P向射线DC方向运动,点Q向射线BD方向运动,设P、Q运动的时间为t(秒),AQ交CD于E.
(1)求抛物线的解析式;
(2)求△APQ的面积S与t的函数关系式;
(3)连接BE.是否存在这样的时刻t,使得∠AEB=∠BDC?若存在请求出t的值;若不存在,请说明理由.

(1)求抛物线的解析式;
(2)求△APQ的面积S与t的函数关系式;
(3)连接BE.是否存在这样的时刻t,使得∠AEB=∠BDC?若存在请求出t的值;若不存在,请说明理由.

分析:(1)利用A,B,C点的坐标,利用交点式求出二次函数的解析式即可;
(2)作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,由(1)中所求A,B,C,D,的坐标,根据三角形相似可求出PF,QG,FG,的长,再利用梯形的面积减去△APF与△AQG的面积即可.
(3)若∠AEB=∠BDC,则根据△AEC∽△EBD,△QED∽△QAB求出t的值.
(2)作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,由(1)中所求A,B,C,D,的坐标,根据三角形相似可求出PF,QG,FG,的长,再利用梯形的面积减去△APF与△AQG的面积即可.
(3)若∠AEB=∠BDC,则根据△AEC∽△EBD,△QED∽△QAB求出t的值.
解答:解:(1)∵抛物线与x轴交于A(6,0),B(19,0),
∴假设解析式为:y=a(x-6)(x-19),
∵抛物线与y轴交于点C(0,8),
∴当x=0时,y=8,
当y=8时,8=a(0-6)(0-19),
∴a=
,
∴抛物线解析式为:y=
(x-6)(x-19)=
x2-
x+8,
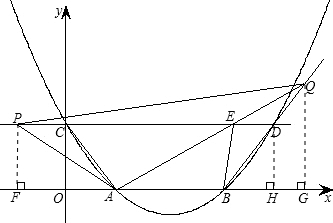
(2)如图,作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,
∵CD∥x轴,
∴PF=DH=OC=8,OH=CD=25,
∵OA=6,OB=19,
∴BH=OH-OB=6,
∴BD=
=10,
∵△BDH∽△BQG,
∴
=
=
.
由题意得CP=DQ=t,AF=t+6,
∴
=
=
,
∴QG=
t+8,BG=
t+6,
∴FG=t+19+
t+6=
t+25.
∴S=S梯形PFGQ-S△PAF-S△AQG=
(PF+QG)•FG-
AF•PF-
BG•QG,
=
t2+8.8t+152.
(3)∵AC=BD=10,
∴四边形ABDC为等腰梯形,
∴∠ACD=∠BDC.
若∠AEB=∠BDC,则∠AEC+∠BED=∠BED+∠EBD,
∴∠AEC=∠EBD.
同理,∠BED=∠EAC.
∴△AEC∽△EBD.
∴
=
,
即
=
,
∴DE=5(DE=20>AB=13舍),
∵△QED∽△QAB,
∴
=
,
即
=
,
解得t=
.
∴假设解析式为:y=a(x-6)(x-19),
∵抛物线与y轴交于点C(0,8),
∴当x=0时,y=8,
当y=8时,8=a(0-6)(0-19),
∴a=
| 4 |
| 57 |
∴抛物线解析式为:y=
| 4 |
| 57 |
| 4 |
| 57 |
| 100 |
| 57 |

(2)如图,作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,
∵CD∥x轴,
∴PF=DH=OC=8,OH=CD=25,
∵OA=6,OB=19,
∴BH=OH-OB=6,
∴BD=
| BH2+DH2 |
∵△BDH∽△BQG,
∴
| BD |
| BQ |
| DH |
| QG |
| BH |
| BG |
由题意得CP=DQ=t,AF=t+6,
∴
| 10 |
| 10+t |
| 8 |
| QG |
| 6 |
| BG |
∴QG=
| 4 |
| 5 |
| 3 |
| 5 |
∴FG=t+19+
| 3 |
| 5 |
| 8 |
| 5 |
∴S=S梯形PFGQ-S△PAF-S△AQG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 2 |
| 5 |
(3)∵AC=BD=10,
∴四边形ABDC为等腰梯形,
∴∠ACD=∠BDC.
若∠AEB=∠BDC,则∠AEC+∠BED=∠BED+∠EBD,
∴∠AEC=∠EBD.
同理,∠BED=∠EAC.
∴△AEC∽△EBD.
∴
| AC |
| DE |
| CE |
| BD |
即
| 10 |
| DE |
| 25-DE |
| 10 |
∴DE=5(DE=20>AB=13舍),
∵△QED∽△QAB,
∴
| ED |
| AB |
| QD |
| QB |
即
| 5 |
| 13 |
| t |
| t+10 |
解得t=
| 25 |
| 4 |
点评:此题主要考查了二次函数的综合应用以及二次函数图象上点的坐标特点及等腰梯形的性质,注意某个图形无法解答时,常常放到其他图形中,利用图形间的“和差“关系求解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC. 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).