题目内容
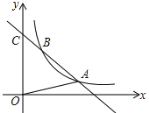
【题目】若抛物线y＝﹣x2+bx+c经过点A（2，0）、B（0，2）．
（1）求这条抛物线的解析式；
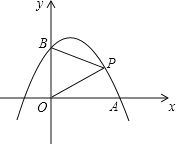
（2）如图，点P是抛物线上一动点，连接BP，OP，若△BOP是以BO为底边的等腰三角形，求点P的坐标．
【答案】（1）y＝﹣x2+x+2；（2）P的坐标为（
，1）或（
，1）．
【解析】
（1）待定系数法求解可得；
（2）根据△BOP是以BO为底边的等腰三角形知点P的纵坐标为1，即可得-x2+x+2=1，解之可得其横坐标．
（1）将点A（2，0），B（0，2）代入y=﹣x2+bx+c，
得：
，
解得：
，
∴这条抛物线的解析式为
；
（2）∵△BOP是以BO为底边的等腰三角形，且OB=2，
∴点P的纵坐标为1，
当
时，
，即
，
解得：
．
∴点P的坐标为（
，1）或（
，1）．
练习册系列答案
相关题目
