题目内容
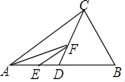
【题目】如图,△ABC是等边三角形,过AB边上点D作DG∥BC,交AC于点G,在GD的延长线上取点E,使ED=CG,连接AE,CD.

(1)求证:AE=DC;
(2)过E作EF∥DC,交BC于点F,求证:∠AEF=∠ACB.
【答案】(1)见解析;(2)见解析
【解析】
(1)通过平行线的性质得△ADG是等边三角形,即可证明![]() ,得证AE=CD;
,得证AE=CD;
(2)根据![]() 可得∠AED=∠DCG,再根据平行线的性质即可得证∠AEF=∠ACB.
可得∠AED=∠DCG,再根据平行线的性质即可得证∠AEF=∠ACB.
解:(1)证明:∵DG∥BC
∴∠ADG=∠AGD=60°
∴△ADG是等边三角形
∴AD=DG,∠ADE=∠DGC=120°,
∵ED=CG,
∴![]()
∴AE=CD
(2)证明:∵![]()
∴∠AED=∠DCG,
∵EF∥CD,
∴∠FEG=∠CDG
∵DG∥BC,
∴∠CDG=∠DCB,
∴∠FEG=∠DCB,
∴∠AEF=∠ACB

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目