题目内容
【题目】如图,在平面直角坐标系中,已知点A(2,3),B(6,3),连接AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤1,则称点P是线段AB的邻近点.
(1)判断点D(![]() ,
,![]() )是否是线段AB的邻近点.________(填是或否);
)是否是线段AB的邻近点.________(填是或否);
(2)若点H(m,n)在一次函数y=x-1的图象上,且是线段AB的邻近点,求m的取值范围;
(3)若一次函数y=x+b的图象上至少存在一个邻近点,直接写出b的取值范围.

【答案】(1)是;(2)3≤m≤5;(3)﹣![]() ﹣3≤b≤
﹣3≤b≤![]() +1
+1
【解析】
(1)根据A、B的坐标得出AB∥x轴,根据点P到直线AB的距离≤1,求出当横坐标2≤x≤6纵坐标2≤y≤4范围内时,点是线段AB的“临近点”,看点的纵坐标是否在y的范围内即可以及在A点的左边到A点的距离≤1,或在B点的右边到B点的距离≤1,点是线段AB的“临近点”;
(2)先求得直线y=x﹣1与线段AB交于(4,3),然后分两种情况讨论:①当m≥4时,根据线段AB的“临近点”的纵坐标的范围是2≤n≤4,把n=2和n=4分别代入n=m﹣1,求出相应的m值,即可得出点的横坐标m的范围;
(3)如图,分别求得N1、N2的坐标,然后根据待定系数法分别求得横坐标为2,纵坐标为3+![]() 或横坐标为6,纵坐标为3﹣
或横坐标为6,纵坐标为3﹣![]() 时,直线y=x+b的b值,依此可求b的取值范围.
时,直线y=x+b的b值,依此可求b的取值范围.
(1)点D是线段AB的“邻近点”;
∵AD= =1,
=1,
∴D(![]() ,
,![]() )是线段AB的“临近点”.
)是线段AB的“临近点”.
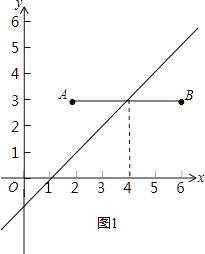
(2)如图1,∵点H(m,n)是线段AB的“邻近点”,点H(m,n)在直线y=x﹣1上,
∴n=m﹣1;
直线y=x﹣1与线段AB交于(4,3)
①当m≥4时,有n=m﹣1≥3,
又AB∥x轴,
∴此时点H(m,n)到线段AB的距离是n﹣3,
∴0≤n﹣3≤1,
∴4≤m≤5,
②当m≤4时,有n=m﹣1,
∴n≤3,
又AB∥x轴,
∴此时点H(m,n)到线段AB的距离是3﹣n,
∴0≤3﹣n≤1,
∴3≤m≤4,
综上所述,3≤m≤5;
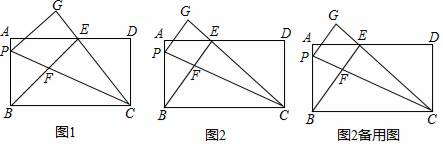
(3)①如图2,
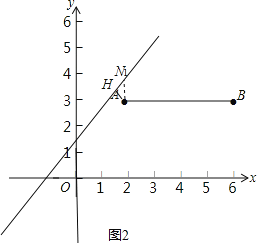
有直线y=x+b可知∠AN1H=45°,
∵AH=1,
∴AN1=![]() ,
,
∴N1(2,3+![]() ),
),
把横坐标2,纵坐标3+![]() 代入直线y=x+b,可得3+
代入直线y=x+b,可得3+![]() =2+b,解得b=
=2+b,解得b=![]() +1;
+1;
②如图3,
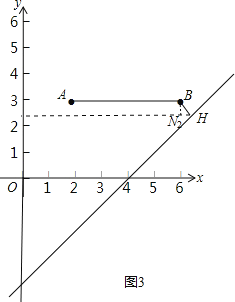
同理证得N2(6,3﹣![]() ),
),
把横坐标6,纵坐标3﹣![]() 代入直线y=x+b,可得3﹣
代入直线y=x+b,可得3﹣![]() =6+b,解得b=﹣
=6+b,解得b=﹣![]() ﹣3;
﹣3;
故b的取值范围为﹣![]() ﹣3≤b≤
﹣3≤b≤![]() +1.
+1.

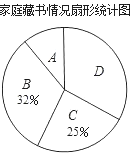
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.