Question

【题目】在正方形中，是边上一点，点在射线上，将线段绕点顺时针旋转得到线段，连接，.

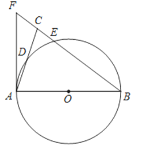
（1）依题意补全图1；

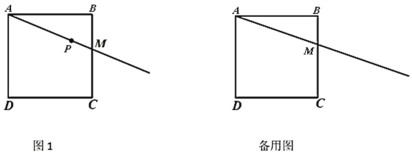
（2）连接，若点，，恰好在同一条直线上，求证：．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据要求画出图形即可；
（2）连接BD，如图2，只要证明△ADQ≌△ABP，∠DPB=90°即可解决问题；

（1）解：补全图形如图1：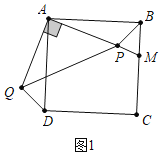

（2）①证明：连接BD，如图2，

∵线段AP绕点A顺时针旋转90°得到线段AQ，
∴AQ=AP，∠QAP=90°，
∵四边形ABCD是正方形，
∴AD=AB，∠DAB=90°，
∴∠1=∠2．
∴△ADQ≌△ABP，
∴DQ=BP，∠Q=∠3，
∵在Rt△QAP中，∠Q+∠QPA=90°，
∴∠BPD=∠3+∠QPA=90°，
∵在Rt△BPD中，DP2+BP2=BD2，
又∵DQ=BP，BD2=2AB2，
∴DP2+DQ2=2AB2．