题目内容
如图①,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,(1)如果△BCE的周长等于50,∠BEC=88°,求BC的长及∠A的度数;
(2)如图②,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC边于点E,若BE=2,∠B=15°.求AC的长.
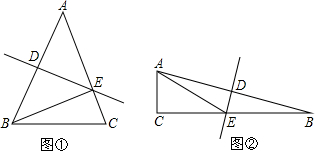
分析:(1)根据线段垂直平分线的性质,得AE=BE,则BC=△BCE的周长-(BE+CE)=△BCE的周长-AC;根据三角形外角的性质和等腰三角形的性质,求得∠A的度数;
(2)根据线段垂直平分线的性质,得AE=BE=2,则∠BAE=∠B=15°;根据三角形外角的性质,得∠AEC=∠B+∠BAE=30°,再根据直角三角形的性质即可求得AC的长.
(2)根据线段垂直平分线的性质,得AE=BE=2,则∠BAE=∠B=15°;根据三角形外角的性质,得∠AEC=∠B+∠BAE=30°,再根据直角三角形的性质即可求得AC的长.
解答:解:(1)∵AB的垂直平分线交AB于点D,交AC于点E,
∴AE=BE,
∴∠A=∠ABE,BE+CE=AC=27.
∴∠A=
∠BEC=44°,BC=50-27=23.
(2)∵AB的垂直平分线交BC边于点E,
∴AE=BE=2,
∴∠BAE=∠B=15°,
∴∠AEC=∠B+∠BAE=30°,
∴AC=
AE=1.
∴AE=BE,
∴∠A=∠ABE,BE+CE=AC=27.
∴∠A=
| 1 |
| 2 |
(2)∵AB的垂直平分线交BC边于点E,
∴AE=BE=2,
∴∠BAE=∠B=15°,
∴∠AEC=∠B+∠BAE=30°,
∴AC=
| 1 |
| 2 |
点评:此题综合运用了线段垂直平分线的性质、等腰三角形的性质、三角形的外角的性质以及直角三角形的性质.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
 明理由.
明理由.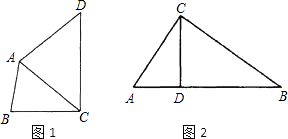
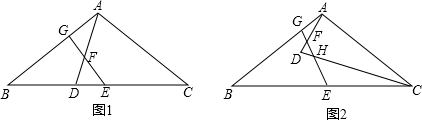
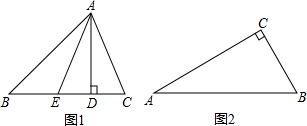 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=