题目内容
如图所示,在梯形ABCD中,AB∥DC,EF是梯形的中位线,AC交EF于G,BD交EF于H,以下说法错误的是( ).
| A.AB∥EF |
| B.AB+DC=2EF |
| C.四边形AEFB和四边形ABCD相似. |
| D.EG=FH |
C.
解析试题分析:根据梯形的中位线的性质进行解答.
在梯形ABCD中,AB∥DC,EF是梯形的中位线,所以AB∥EF,故A正确;
因为EF是梯形ABCD的中位线,所以EG=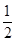 CD,GF=
CD,GF=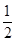 AB,故EF=
AB,故EF=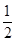 CD+
CD+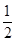 AB,即AB+DC=2EF,故B正确.
AB,即AB+DC=2EF,故B正确.
在四边形AEFB和四边形ABCD中,对应角相等,对应边不成比例,因此四边形AEFB和四边形ABCD不相似.故C错误;
由于EG、HF分别是△ACD、△BCD的中位线,知EG=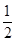 CD,HF=
CD,HF=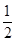 CD,所以EG=FH,故D正确.
CD,所以EG=FH,故D正确.
故选C.
考点: 梯形的中位线.

练习册系列答案
相关题目
下列命题中,正确的是( )
| A.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边; |
| B.不同向量的单位向量的长度都相等,方向也都相同; |
| C.相似三角形的中线的比等于相似比; |
| D.一般来说,一条线段的黄金分割点有两个. |
下列各组中的四条线段成比例的是( )
| A.4cm、2cm、1cm、3cm | B.1cm、2cm、3cm、5cm |
| C.3cm、4cm、5cm、6cm | D.1cm、2cm、2cm、4cm |
如图所示,E为□ABCD的边AD上的一点,且AE∶ED=3∶2,CE交BD于F,则BF∶FD ( )
| A.3∶5 | B.5∶3 | C.2∶5 | D.5∶2 |
如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )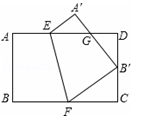
| A.3:2 | B.9:4 | C.4:3 | D.16:9 |
已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积之比为【 】
| A.4:3 | B.3:4 | C.16:9 | D.9:16 |
 中,
中, ,当直角三角板
,当直角三角板 的
的 角的顶点
角的顶点 在
在 上移动时,斜边
上移动时,斜边 始终经过
始终经过 边的中点
边的中点 ,设直角三角板的另一直角边
,设直角三角板的另一直角边 与
与 相交于点E.设
相交于点E.设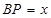 ,
, ,那么
,那么 与
与 之间的函数图象大致是( )
之间的函数图象大致是( )

 AE,垂足为G,BG=
AE,垂足为G,BG=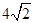 ,则△CEF的周长为( )
,则△CEF的周长为( )




