题目内容
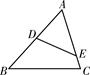
如图所示，E为□ABCD的边AD上的一点，且AE∶ED＝3∶2，CE交BD于F，则BF∶FD （ ）
| A．3∶5 | B．5∶3 | C．2∶5 | D．5∶2 |
C.
解析试题分析：由在?ABCD中，且BE：EC=2：3，易得BE：AD=2：5，△ADF∽△EBF，然后根据相似三角形的对应边成比例，即可求得答案．
∵BE：EC=2：3，
∴BE：BC=2：5，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴BE：AD=2：5，△ADF∽△EBF，
∴
．
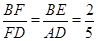故选C.
考点: 1.相似三角形的判定与性质；2.平行四边形的性质．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（ ）
A．a= b | B．a=2b | C．a=2b | D．a=4b |
相似的是（ ）
如图所示，在梯形ABCD中，AB∥DC，EF是梯形的中位线，AC交EF于G，BD交EF于H，以下说法错误的是（ ）.
| A．AB∥EF |
| B．AB+DC=2EF |
| C．四边形AEFB和四边形ABCD相似. |
| D．EG=FH |
如图，在平行四边形ABCD中，E为CD上一点，DE：CE=2：3，连结AE、BE、BD且AE，BD交于点F，则S△DEF：S△ADF：S△ABF等于（ ）
| A．2：3：5 | B．4：9：25 | C．4：10：25 | D．2：5：25 |
