题目内容
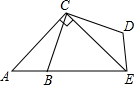
如图，△ACE是等腰直角三角形，B为AE上一点，△ABC经过旋转到达△EDC的位置，若AC=2
，DE=1，则BE=______，BC=______．
| 2 |
∵△ACE是等腰直角三角形，AC=2
，
∴CE=2
，AE=
=
=4，
∵△ABC经过旋转到达△EDC的位置，DE=1，
∴AB=1，
∴BE=4-1=3；
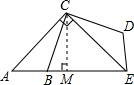
过点C作CM⊥BE于点M，
∵AC=EC，∠A=∠CEA=45°，
∴∠ACM=∠ECM=45°，
∴AM=CM=EM=
AE=2，
∵AB=1，
∴BM=2-1=1，
∴BC=
=
=
．
故答案为：3，
．
| 2 |
∴CE=2
| 2 |
| AC2+EC2 |
| 8+8 |
∵△ABC经过旋转到达△EDC的位置，DE=1，
∴AB=1，
∴BE=4-1=3；
过点C作CM⊥BE于点M，
∵AC=EC，∠A=∠CEA=45°，
∴∠ACM=∠ECM=45°，
∴AM=CM=EM=
| 1 |
| 2 |
∵AB=1，
∴BM=2-1=1，
∴BC=
| BM2+CM2 |
| 12+22 |
| 5 |
故答案为：3，
| 5 |
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
