题目内容
【题目】在△ABC中,AB=6,AC=8,BC=10,D是△ABC内部或BC边上的一个动点(与B、C不重合),以D为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF∥BC.
(1)求∠D的度数;
(2)若两三角形重叠部分的形状始终是四边形AGDH.
①如图1,连接GH、AD,当GH⊥AD时,请判断四边形AGDH的形状,并证明;
②当四边形AGDH的面积最大时,过A作AP⊥EF于P,且AP=AD,求k的值.
【答案】
(1)
解:∵AB2+AC2=100=BC2,
∴∠BAC=90°,
∵△DEF∽△ABC,
∴∠D=∠BAC=90°
(2)
解:①四边形AGDH为正方形,
理由:如图1,
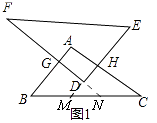
延长ED交BC于M,延长FD交BC于N,
∵△DEF∽△ABC,
∴∠B=∠C,
∵EF∥BC,
∴∠E=∠EMC,
∴∠B=∠EMC,
∴AB∥DE,
同理:DF∥AC,
∴四边形AGDH为平行四边形,
∵∠D=90°,
∴四边形AGDH为矩形,
∵GH⊥AD,
∴四边形AGDH为正方形;
②当点D在△ABC内部时,四边形AGDH的面积不可能最大,
理由:如图2,
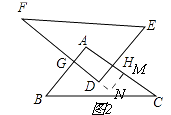
点D在内部时(N在△ABC内部或BC边上),延长GD至N,过N作NM⊥AC于M,
∴矩形GNMA面积大于矩形AGDH,
∴点D在△ABC内部时,四边形AGDH的面积不可能最大,
只有点D在BC边上时,面积才有可能最大,
如图3,
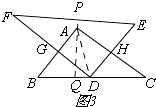
点D在BC上,
∵DG∥AC,
∴△BGD∽△BAC,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴AH=8﹣ ![]() GA,
GA,
S矩形AGDH=AG×AH=AG×(8﹣ ![]() AG)=﹣
AG)=﹣ ![]() AG2+8AG,
AG2+8AG,
当AG=﹣ ![]() =3时,S矩形AGDH最大,此时,DG=AH=4,
=3时,S矩形AGDH最大,此时,DG=AH=4,
即:当AG=3,AH=4时,S矩形AGDH最大,
在Rt△BGD中,BD=5,
∴DC=BC﹣BD=5,
即:点D为BC的中点,
∵AD= ![]() BC=5,
BC=5,
∴PA=AD=5,
延长PA,∵EF∥BC,QP⊥EF,
∴QP⊥BC,
∴PQ是EF,BC之间的距离,
∴D是EF的距离为PQ的长,
在△ABC中, ![]() AB×AC=
AB×AC= ![]() BC×AQ
BC×AQ
∴AQ=4.8
∵△DEF∽△ABC,
∴k= ![]()
【解析】(1)先判断△ABC是直角三角形,即可;(2)①先判断AB∥DE,DF∥AC,得到平行四边形,再判断出是正方形;
②先判断面积最大时点D的位置,由△BGD∽△BAC,找出AH=8﹣ ![]() GA,得到S矩形AGDH=﹣
GA,得到S矩形AGDH=﹣ ![]() AG2+8AG,确定极值,AG=3时,面积最大,最后求k得值.此题是相似三角形的综合题,主要考查了相似三角形的性质和判定,平行四边形,矩形,正方形的判定和性质,极值的确定,勾股定理的逆定理,解本题的关键是作出辅助线,
AG2+8AG,确定极值,AG=3时,面积最大,最后求k得值.此题是相似三角形的综合题,主要考查了相似三角形的性质和判定,平行四边形,矩形,正方形的判定和性质,极值的确定,勾股定理的逆定理,解本题的关键是作出辅助线,
【考点精析】利用平行线的性质和相似三角形的性质对题目进行判断即可得到答案,需要熟知两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;对应角相等,对应边成比例的两个三角形叫做相似三角形.

 应用题作业本系列答案
应用题作业本系列答案【题目】如图1,在△ABC中,点D在边BC上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O是△ABD的外接圆. 
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图2),求∠CAD的度数.
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.