��Ŀ����
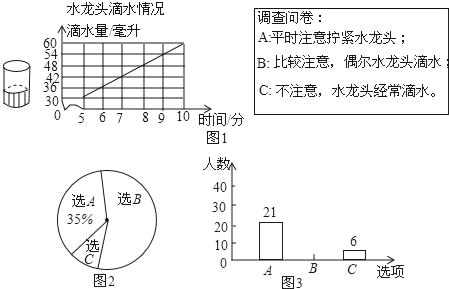
����Ŀ��ij��ʵʩ�����ͨ�������У�������A��B����֮������һ����·���ס����������̶ӷֱ��A��B����ͬʱ��ʼ������ʩ���ڼ䣬�Ҷ�������������ǰ�뿪�����µ������ɼӵ�����ɣ�ֱ����·��ͨ����ͼ�Ǽס����������̶���·����y���ף�������ʱ��x���죩֮��ĺ���ͼ�������ͼ�����ṩ����Ϣ������������⣺
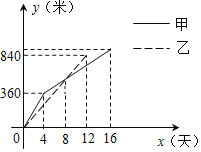
��1��д���ҹ��̶���·�ij���y������ʱ��x֮��ĺ�����ϵʽ��_____��
��2�����̶�ǰ8������·Ϊ_____�ף��ù�·���ܳ���Ϊ_____�ף�
��3�����ҹ��̶Ӳ���ǰ�뿪��������ֻ��_____������������
��4���ס��������̶ӵ�_____��ʱ����·�ij������80�ף�
���𰸡�y��70x 560 1800 13 4��12��![]()
��������
��1�������������������ʽ���ѣ�12��840������ɵ�����������ʽ��
��2����ǰ4����·����·�̳���4���ɵõ����̶�ǰ4��ƽ��ÿ����·��������ü��ڵ�4�쵽��16��ĺ�������ʽ��������ú�12����·����·�̣�����12��Ϊ��12��ƽ����·�������������ó����̶�ǰ8������·��·�̣��ü���·����·��+����·����·�̼�Ϊ��·���ܳ��ȣ�
��3����������������������Ч��������ʱ������ʽ���㼴����⣻
��4�����������з��̽�ɣ�
�⣺��1����y��kx��
�߾�����12��840����
��12k��840��
���k��70��
��y��70x��
�ʴ�Ϊy��70x��
��2�����̶�ǰ4��ƽ��ÿ����·����Ϊ360��4��90��
��x��8ʱ��y��560��
�赱4��x��16ʱ�����̶ӵĺ�������ʽΪy��kx+b��
![]() ��
��
���![]() ��
��
��y��50x+160��
��x��16ʱ��y��960��
���12��ƽ��ÿ����·����Ϊ��960��360����12��50��
����̶�ǰ8������·Ϊ��360+50����8��4����560���ף���
��·���ܳ���Ϊ840+960��1800���ף���
�ʴ�Ϊ560��1800
��3�����ҹ��̶Ӳ���ǰ�뿪����������Ҫ��ʱ��Ϊ��12+��1800��840��2������50+70����13���죩��
�ʴ�Ϊ��13��
��4����ס��������̶ӵ�x��ʱ����·�ij������80�ף����������
90x��70x��80��70x��[360+50��x��4��]��80��50��x��4��+360��840+80��
���x��4��12��![]() ��
��
�ʴ�Ϊ��4��12��![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��������20�����ˣ�ij�������������������ͳ�����±���
����20������ijһ���������������ͳ�Ʊ�
��������ĸ��������� | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
�����������ˣ� | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
��1������һ��20���������������ƽ��������
��2��Ϊ����ߴ�������˵Ļ����ԣ���������ʵ�С�ÿ�춨�������������н����Ĵ�ʩ��������ǹ����ߣ���ƽ��������λ���������ĽǶȽ��з������㽫���ȷ������������