题目内容
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD =∠BCE = 90°,点M为AN的中点,过点E与AD平行的直线交射线AM于点N。
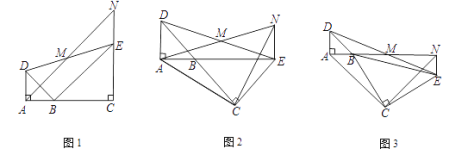
(1)当A,B,C三点在同一直线上时(如图1),求证:AD=NE ;
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,请证明;若不成立,请说明理由。
【答案】(1)见解析;(2)见解析;(3)成立,证明见解析
【解析】
(1)由EN∥AD,点M为AN的中点,利用AAS证得△ADM≌△NEM,从而得到结论;
(2)易证AB=DA=NE,∠ABC=∠NEC=135°,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形;
(3)借鉴(2)中的解题经验可得AB=DA=NE,∠ABC=∠NEC=180°-∠CBN,从而可以证到△ABC≌△NEC,进而可以证到AC=NC,∠ACN=∠BCE=90°,则有△ACN为等腰直角三角形.
(1)如图1,
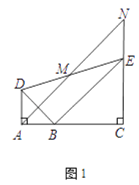
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为AN的中点,
∴AM=MN.
在△ADM和△NEM中,
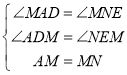
∴△ADM≌△NEM(AAS).
∴AD=NE;
(2)如图2,
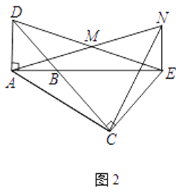
∵![]() BAD和△BCE均为等腰直角三角形,
BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°.
∵AD∥NE,∴∠DAE+∠NEA=180°.
∵∠DAE=90°,∴∠NEA=90°.
∴∠NEC=135°.
∵A,B,E三点在同一直线上,
∴∠ABC=180°﹣∠CBE=135°.
∴∠ABC=∠NEC.
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM.
∵点M为AN的中点,
∴AM=MN.
在△ADM和△NEM中,
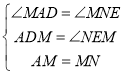
∴△ADM≌△NEM(AAS).
∴AD=NE.
又∵AD=AB,∴AB=NE.
在△ABC和△NEC中,
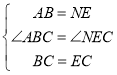
∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.
(3)△ACN仍为等腰直角三角形.
如图3,
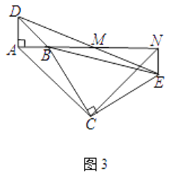
此时A、B、N三点在同一条直线上.
∵AD∥EN,∠DAB=90°,∴∠ENA=∠DAN=90°.
∵∠BCE=90°,∴∠CBN+∠CEN=360°﹣90°﹣90°=180°.
∵A、B、N三点在同一条直线上,∴∠ABC+∠CBN=180°.
∴∠ABC=∠NEC.
∵△ADM≌△NEM(已证),AD=NE.
又∵AD=AB,∴AB=NE.
在△ABC和△NEC中,
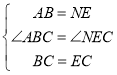
∴△ABC≌△NEC(SAS).
∴AC=NC,∠ACB=∠NCE.
∴∠ACN=∠BCE=90°.
∴△ACN为等腰直角三角形.

【题目】车间有20名工人,某天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) | 9 | 10 | 11 | 12 | 13 | 15 | 16 | 19 | 20 |
工人人数(人) | 1 | 1 | 6 | 4 | 2 | 2 | 2 | 1 | 1 |
(1)求这一天20名工人生产零件的平均个数;
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?