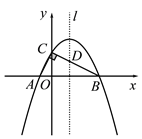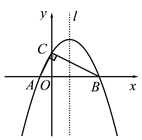题目内容
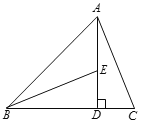
【题目】感知:如图①,在正方形ABCD中,点E在对角线AC上(不与点A、C重合),连结ED,EB,过点E作EF⊥ED,交边BC于点F.易知∠EFC+∠EDC=180°,进而证出EB=EF.
探究:如图②,点E在射线CA上(不与点A、C重合),连结ED、EB,过点E作EF⊥ED,交CB的延长线于点F.求证:EB=EF
应用:如图②,若DE=2,CD=1,则四边形EFCD的面积为

【答案】探究:证明见详解;应用:![]()
【解析】
探究:根据正方形的性质得到AB=BC=CD=DA,∠ABC=∠ADC=∠BCD=90°.求得∠ACB=∠ACD=45°,根据全等三角形的性质得到ED=EB,∠EDC=∠EBC,求得∠EFB=∠EDC,根据等腰三角形的判定定理即可得到结论;
应用:连接DF,求得△DEF是等腰直角三角形,根据勾股定理得到CF=![]() ,由三角形的面积公式即可得到结论.
,由三角形的面积公式即可得到结论.
解:探究:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠ADC=∠BCD=90°.
∴∠ACB=∠ACD=45°,
又∵EC=EC,
∴△EDC≌△EBC(SAS),
∴ED=EB,∠EDC=∠EBC,
∵EF⊥ED,
∴∠DEF=90°,
∴∠EFC+∠EDC=180°
又∵∠EBC+∠EBF=180°,
∴∠EFB=∠EDC,
∴∠EBF=∠EFB,
∴EB=EF;
应用:连接DF,

∵EF=DE,∠DEF=90°,
∴△DEF是等腰直角三角形,
∵DE=2,
∴EF=2,DF=![]() ,
,
∵∠DCB=90°,CD=1,
∴CF=![]() ,
,
∴四边形EFCD的面积=S△DEF+S△CDF=![]() .
.
故答案为:![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目