题目内容
【题目】圆内接正三角形、正方形、正六边形的边长之比为( )
A.1：2：3B.1：
：
C.：：1D.无法确定
【答案】C
【解析】
根据题意画出图形，设出圆的半径，再由正多边形及直角三角形的性质求解即可．
解：设圆的半径为R，
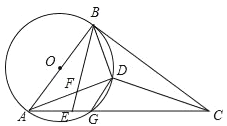
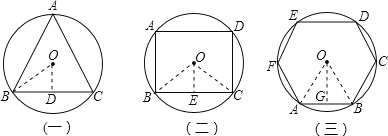
如图(一)，
连接OB，过O作OD⊥BC于D，
则∠OBC=30°，BD=OBcos30°
R，
故BC=2BD
R；
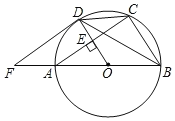
如图(二)，
连接OB、OC，过O作OE⊥BC于E，
则△OBE是等腰直角三角形，
2BE2=OB2，即BE
，
故BC
R；
如图(三)，
连接OA、OB，过O作OG⊥AB，
则△OAB是等边三角形，
故AG=OAcos60°
R，AB=2AG=R，
∴圆内接正三角形、正方形、正六边形的边长之比为
R：
R：R：：1．
故选：C．
练习册系列答案
相关题目
【题目】在如图中，每个正方形有边长为1 的小正方形组成：
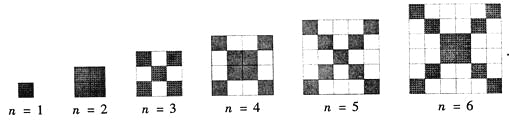
（1） 观察图形，请填写下列表格：
正方形边长 | 1 | 3 | 5 | 7 | … | n(奇数) |
黑色小正方形个数 | … | |||||
正方形边长 | 2 | 4 | 6 | 8 | … | n(偶数) |
黑色小正方形个数 | … |
（2）在边长为n（n≥1）的正方形中，设黑色小正方形的个数为P1，白色小正方形的个数为P2，问是否存在偶数n，使P2＝5P1？若存在，请写出n的值；若不存在，请说明理由.
