题目内容
【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
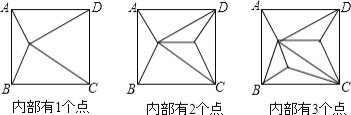
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
【答案】(1) 8,10 ,2n+2;(2)不行,理由见解析.
【解析】
(1)由图形中三角形的个数,并观察发现,每多一个点,三角形的个数增加2,然后据此规律填表即可;
(2)根据(1)中规律,列式求解,如果n是整数,则能分割,如果不是整数,则不能分割.
解:(1)有1个点时,内部分割成4个三角形;
有2个点时,内部分割成6=4+2个三角形;
有3个点时,内部分割成8=4+2×2个三角形;
有4个点时,内部分割成10=4+2×3个三角形;…
以此类推,有n个点时,内部分割成4+2×(n-1)=(2n+2)个三角形,
补全表格如下:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | 8 | 10 | … | 2n+2 |
(2)不能,
由(1)知2n+2=2019,
解得:n=1008![]() ,不是整数,所以不能分割成2019个三角形.
,不是整数,所以不能分割成2019个三角形.

练习册系列答案
相关题目