题目内容
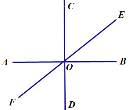
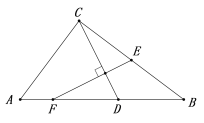
【题目】如图：在△ABC中，∠ACB ＝90°，点D在边AB上，AD＝AC，点E在BC边上，CE＝BD，过点E作EF⊥CD交AB于点F，若AF＝2，BC＝8，则DF的长为_______
【答案】4
【解析】
延长AC至点G，使AG=AB，延长EF、CA交于H，根据题意证明△CEH≌CGB，即可得到DF=AD-AF=AC-AH=CH-2AF=BC-2AF，即可求解.
设∠BCD=a,∵∠ACB=90°，∴∠ACD=90°-a，∵AD=AC,∴∠ADC=∠ACD=90°-a，∴∠CAB=2a,∴∠ABC=90°-2a,
∵EF⊥CD,∴∠DKF=90°，∴∠DFK=a，∴∠CEF=90°-a,
延长AC至点G，使AG=AB，连接BG,∴∠G=90°-a=∠CEF，
∵AC=AD,∴BD=CG=CE,
延长EF、CA交于H，
∴∠H=a=∠BFE=∠AFH，
∴AH=AF=2，
∵∠ACB=∠BCG=90°，CG=CE，∠G=∠CEF
∴△CEH≌CGB
∴BC=CH=8，
∴DF=AD-AF=AC-AH=CH-2AF=BC-2AF=4.
故填：4.
【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售，其进价与标价如下表：
LED 灯泡 | 普通白炽灯泡 | |
进价（元） | 45 | 25 |
标价（元） | 60 | 30 |
（1）该商场购进了 LED 灯泡与普通白炽灯泡共 300 个，LED 灯泡按标价进行销售，而普通 白炽灯泡打九折销售，当销售完这批灯泡后可获利 3 200 元，求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个？
（2）由于春节期间热销，很快将两种灯泡销售完，若该商场计划再次购进这两种灯泡 120 个， 在不打折的情况下，请问如何进货，销售完这批灯泡时获利最多且不超过进货价的 30%， 并求出此时这批灯泡的总利润为多少元？
