Question

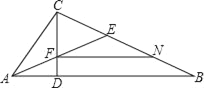
【题目】如图，在△ABC中，CD⊥AB，且CD2=ADDB，AE平分∠CAB交CD于F，∠EAB=∠B，CN=BE．①CF=BN；②∠ACB=90°；③FN∥AB；④AD2=DFDC．则下列结论正确的是（　　）

A. ①②④ B. ②③④ C. ①②③④ D. ①③

Answer 1

【答案】C

【解析】

根据已知条件可证△ADC∽△CDB，得出∠ACB=90°．根据等量关系及等腰三角形的性质得到CF=BN．根据同位角相等，证明FN∥AB．证明△ADF∽△CDA，根据相似三角形的性质得出AD2=DFDC．

①∵AE平分∠CAB，

∴∠CAE=∠DAF，

∴△CAE∽△DAF，

∴∠AFD=∠AEC，

∴∠CFE=∠AEC，

∴CF=CE，

∵CN=BE，

∴CE=BN，

∴CF=BN，故本选项正确；

②∵CD⊥AB，

∴∠ADC=∠CDB=90°，

∵CD2=ADDB，

∴，

∴△ADC∽△CDB，

∴∠ACD=∠B，

∴∠ACB=90°，故本选项正确；

③∵∠EAB=∠B，

∴EA=EB，

易知：∠ACF=∠ABC=∠EAB=∠EAC，

∴FA=FC，

易证：CF=CE，

∴CF=AF=CE，

∵FA=FC=BN，EA=EB，

∴EF=CE，

∴,

∵∠FEN=∠AEB，

∴△EFN∽△EAB，

∴∠EFN=∠EAB，

∴FN∥AB，故本选项正确；

④易证△ADF∽△CDA，

∴AD2=DFDC，故本选项正确；

故选：C．