题目内容
【题目】回答问题:
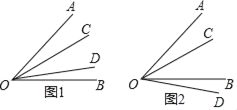
(1)已知∠AOB的度数为54°,在∠AOB的内部有一条射线OC,满足∠AOC=![]() ∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=
∠COB,在∠AOB所在平面上另有一条射线OD,满足∠BOD=![]() ∠AOC,如图1和图2所示,求∠COD的度数.
∠AOC,如图1和图2所示,求∠COD的度数.
(2)已知线段AB长为12cm,点C是线段AB上一点,满足AC=![]() CB,点D是直线AB上满足BD=
CB,点D是直线AB上满足BD=![]() AC.请画出示意图,求出线段CD的长.
AC.请画出示意图,求出线段CD的长.
【答案】(1) ∠COD的度数为27°或45°,(2)线段CD的长是6cm或10cm
【解析】
(1)分两种情况讨论:①当OD在∠COB内时,②当OD在∠COB外时.根据角的倍分关系先求出∠AOC、∠COB的度数,进一步得到∠BOD的度数,再根据角的和差关系可求∠COD的度数.
(2)分两种情况讨论:①当D在线段CB上时,②当D在线段CB的延长线时.由AB的长,即AC为BC的一半求出AC与BC的长,再由BD为AC一半求出BD的长,由BC﹣BD及BD+BC即可求出CD的长.
(1)分两种情况讨论:①当OD在∠COB内时,如图1.
∵∠AOB的度数为54°,∠AOC=![]() ∠COB,∴∠AOC=18°,∠COB=36°.
∠COB,∴∠AOC=18°,∠COB=36°.
∵∠BOD=![]() ∠AOC,∴∠BOD=9°,∴∠COD=36°-9°=27°;
∠AOC,∴∠BOD=9°,∴∠COD=36°-9°=27°;
②当OD在∠COB外时,如图2.
∵∠AOB的度数为54°,∠AOC=![]() ∠COB,∴∠AOC=18°,∠COB=36°.
∠COB,∴∠AOC=18°,∠COB=36°.
∵∠BOD=![]() ∠AOC,∴∠BOD=9°,∴∠COD=36°+9°=45°;
∠AOC,∴∠BOD=9°,∴∠COD=36°+9°=45°;
综上所述:∠COD的度数为27°或45°.
(2))由题意得:AC=4cm,BC=8cm,BD=2cm.分两种情况讨论:
①当D在线段CB上时,如图1,则CD=BC﹣BD=6(cm);
②当D在线段CB的延长线时,如图2,则CD=BC+BD=10(cm).
综上所述:线段CD的长是6cm或10cm.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】三五三七鞋厂为了了解初中学生穿鞋的鞋号情况,对红华中学初二(1)班的20名男生所穿鞋号统计如下表:
鞋号 | 23.5 | 24 | 24.5 | 25 | 25.5 | 26 |
人数 | 3 | 4 | 4 | 7 | 1 | 1 |
(1)写出男生鞋号数据的平均数,中位数,众数;
(2)在平均数,中位数和众数中,鞋厂最感兴趣的是什么?